In a class 140 students numbered 1 to 140, all even numbered students opted Mathematics course, those whose number is divisible by 3 opted Physics course and those whose number is divisible by 5 opted Chemistry course. Then the number of students who did not opt for any of the three courses is (a) 38 (b) 1 (c)42 (d) 102
To solve the problem, we need to determine how many students did not opt for any of the three courses: Mathematics, Physics, or Chemistry. We will use the principle of inclusion-exclusion to find the number of students enrolled in at least one course.
Step 1: Count the students opting for Mathematics
All even-numbered students opted for Mathematics. The even numbers from 1 to 140 are:
2, 4, 6, ..., 140.
To find the number of even numbers, we can use the formula for the nth term of an arithmetic sequence:
- First term (a) = 2
- Common difference (d) = 2
- Last term (l) = 140
The number of terms (n) can be calculated as:
n=l−ad+1=140−22+1=70.
So, 70 students opted for Mathematics.
Step 2: Count the students opting for Physics
Students whose numbers are divisible by 3 opted for Physics. The numbers divisible by 3 from 1 to 140 are:
3, 6, 9, ..., 138.
Using the same formula:
- First term (a) = 3
- Common difference (d) = 3
- Last term (l) = 138
The number of terms (n) is:
n=l−ad+1=138−33+1=46.
So, 46 students opted for Physics.
Step 3: Count the students opting for Chemistry
Students whose numbers are divisible by 5 opted for Chemistry. The numbers divisible by 5 from 1 to 140 are:
5, 10, 15, ..., 140.
Using the formula:
- First term (a) = 5
- Common difference (d) = 5
- Last term (l) = 140
The number of terms (n) is:
n=l−ad+1=140−55+1=28.
So, 28 students opted for Chemistry.
Step 4: Count the students opting for both Mathematics and Physics
Students who opted for both Mathematics and Physics are those whose numbers are divisible by both 2 and 3 (i.e., divisible by 6). The numbers divisible by 6 from 1 to 140 are:
6, 12, 18, ..., 138.
Using the formula:
- First term (a) = 6
- Common difference (d) = 6
- Last term (l) = 138
The number of terms (n) is:
n=l−ad+1=138−66+1=23.
So, 23 students opted for both Mathematics and Physics.
Step 5: Count the students opting for both Mathematics and Chemistry
Students who opted for both Mathematics and Chemistry are those whose numbers are divisible by both 2 and 5 (i.e., divisible by 10). The numbers divisible by 10 from 1 to 140 are:
10, 20, 30, ..., 140.
Using the formula:
- First term (a) = 10
- Common difference (d) = 10
- Last term (l) = 140
The number of terms (n) is:
n=l−ad+1=140−1010+1=14.
So, 14 students opted for both Mathematics and Chemistry.
Step 6: Count the students opting for both Physics and Chemistry
Students who opted for both Physics and Chemistry are those whose numbers are divisible by both 3 and 5 (i.e., divisible by 15). The numbers divisible by 15 from 1 to 140 are:
15, 30, 45, ..., 135.
Using the formula:
- First term (a) = 15
- Common difference (d) = 15
- Last term (l) = 135
The number of terms (n) is:
n=l−ad+1=135−1515+1=9.
So, 9 students opted for both Physics and Chemistry.
Step 7: Count the students opting for all three courses
Students who opted for all three courses are those whose numbers are divisible by 2, 3, and 5 (i.e., divisible by 30). The numbers divisible by 30 from 1 to 140 are:
30, 60, 90, 120.
Using the formula:
- First term (a) = 30
- Common difference (d) = 30
- Last term (l) = 120
The number of terms (n) is:
n=l−ad+1=120−3030+1=4.
So, 4 students opted for all three courses.
Step 8: Apply the principle of inclusion-exclusion
Let:
- |M|=70 (students opting for Mathematics)
- |P|=46 (students opting for Physics)
- |C|=28 (students opting for Chemistry)
- |M∩P|=23 (students opting for both Mathematics and Physics)
- |M∩C|=14 (students opting for both Mathematics and Chemistry)
- |P∩C|=9 (students opting for both Physics and Chemistry)
- |M∩P∩C|=4 (students opting for all three courses)
Using the inclusion-exclusion principle:
|M∪P∪C|=|M|+|P|+|C|−|M∩P|−|M∩C|−|P∩C|+|M∩P∩C|
Substituting the values:
|M∪P∪C|=70+46+28−23−14−9+4=102.
Step 9: Calculate the number of students not opting for any course
The total number of students is 140. Therefore, the number of students who did not opt for any course is:
140−|M∪P∪C|=140−102=38.
Final Answer
The number of students who did not opt for any of the three courses is 38.
---
All even-numbered students opted for Mathematics. The even numbers from 1 to 140 are:
2, 4, 6, ..., 140.
- First term (a) = 2
- Common difference (d) = 2
- Last term (l) = 140
n=l−ad+1=140−22+1=70.
Students whose numbers are divisible by 3 opted for Physics. The numbers divisible by 3 from 1 to 140 are:
3, 6, 9, ..., 138.
- First term (a) = 3
- Common difference (d) = 3
- Last term (l) = 138
n=l−ad+1=138−33+1=46.
Students whose numbers are divisible by 5 opted for Chemistry. The numbers divisible by 5 from 1 to 140 are:
5, 10, 15, ..., 140.
- First term (a) = 5
- Common difference (d) = 5
- Last term (l) = 140
n=l−ad+1=140−55+1=28.
Students who opted for both Mathematics and Physics are those whose numbers are divisible by both 2 and 3 (i.e., divisible by 6). The numbers divisible by 6 from 1 to 140 are:
6, 12, 18, ..., 138.
- First term (a) = 6
- Common difference (d) = 6
- Last term (l) = 138
n=l−ad+1=138−66+1=23.
Students who opted for both Mathematics and Chemistry are those whose numbers are divisible by both 2 and 5 (i.e., divisible by 10). The numbers divisible by 10 from 1 to 140 are:
10, 20, 30, ..., 140.
- First term (a) = 10
- Common difference (d) = 10
- Last term (l) = 140
n=l−ad+1=140−1010+1=14.
Students who opted for both Physics and Chemistry are those whose numbers are divisible by both 3 and 5 (i.e., divisible by 15). The numbers divisible by 15 from 1 to 140 are:
15, 30, 45, ..., 135.
- First term (a) = 15
- Common difference (d) = 15
- Last term (l) = 135
n=l−ad+1=135−1515+1=9.
Students who opted for all three courses are those whose numbers are divisible by 2, 3, and 5 (i.e., divisible by 30). The numbers divisible by 30 from 1 to 140 are:
30, 60, 90, 120.
- First term (a) = 30
- Common difference (d) = 30
- Last term (l) = 120
n=l−ad+1=120−3030+1=4.
Let:
- |M|=70 (students opting for Mathematics)
- |P|=46 (students opting for Physics)
- |C|=28 (students opting for Chemistry)
- |M∩P|=23 (students opting for both Mathematics and Physics)
- |M∩C|=14 (students opting for both Mathematics and Chemistry)
- |P∩C|=9 (students opting for both Physics and Chemistry)
- |M∩P∩C|=4 (students opting for all three courses)
|M∪P∪C|=|M|+|P|+|C|−|M∩P|−|M∩C|−|P∩C|+|M∩P∩C|
Substituting the values:
|M∪P∪C|=70+46+28−23−14−9+4=102.
The total number of students is 140. Therefore, the number of students who did not opt for any course is:
140−|M∪P∪C|=140−102=38.
The number of students who did not opt for any of the three courses is 38.
Similar Questions

What is the number of students who opted for dancing ?
View SolutionIn a class of 80 students numbered 1 to 80, all even numbered students opt for physics, whose numbers are divisible by 5 opt for chemistry and those who are divisible by 7 opt for mathematics. Number of students who offered mathematics
View Solution
Knowledge Check
In the IGNOU (Indira Gandhi National Open University) there are total 16,000 students pursuing MBA, which offers the specialization only in Finance, HR and Marketing IGNOU accepts only Science, Commerce and Engineering Students for the two years course of MBA. The number of science. students is 166.66% of the Commerce students. Number of Engineering students is equal to the number of Science and Commerce students together. Each student can specialize in only one of the marketing , HR and Finance, 20% of Science students opted the Finance, which is 16.66% less than the no. of commerce students who opted Finance. The total Finance students is equal to 18% the total strength of the MBA students. 32% of Science students opted HR. Commerce students who opted HR is equal to 25% of total students specializing in Finance and Engineering students equal to 6.5% of the total strength of the MBA students opted HR.
The number of Engineering students who opted marketing is :A7850B7500C8850Dnone of theseA class has 172 students. The following data shows the number of students opting one or more subjects: Mathematics 125, Physics 95, Chemistry 65 Mathematics and Physics 55
Mathematics and Chemistry 53
Physics and Chemistry 48 Mathematics, Physics and Chemistry 43
The number of students who opted only Physics isA35B45C29D37There are 20 students in a chemistry class and 30 students in a physics class. If ten students are to be enrolled in both the courses, then the number of students which are either in physics class or chemistry class is
A50, if two classes meet at the same hourB40, if two classes meet at different hoursCboth (a) and (b) correctD(a) correct but (b) incorrect

Find the central angle of total number of students who opted for History ?
View Solution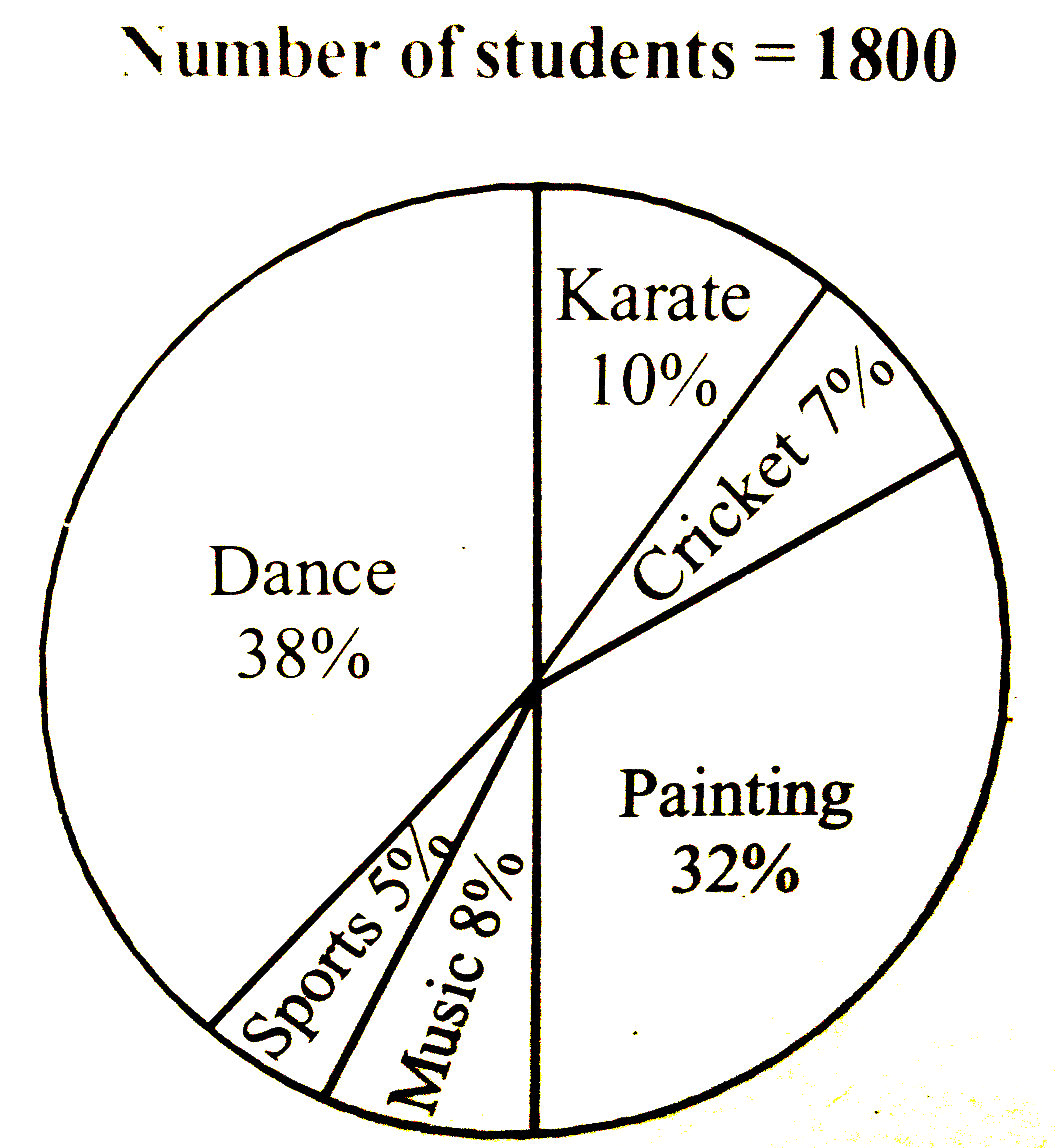
What is the respective ratio between the number of students who opted for dancing and karate who opted for painting
View Solution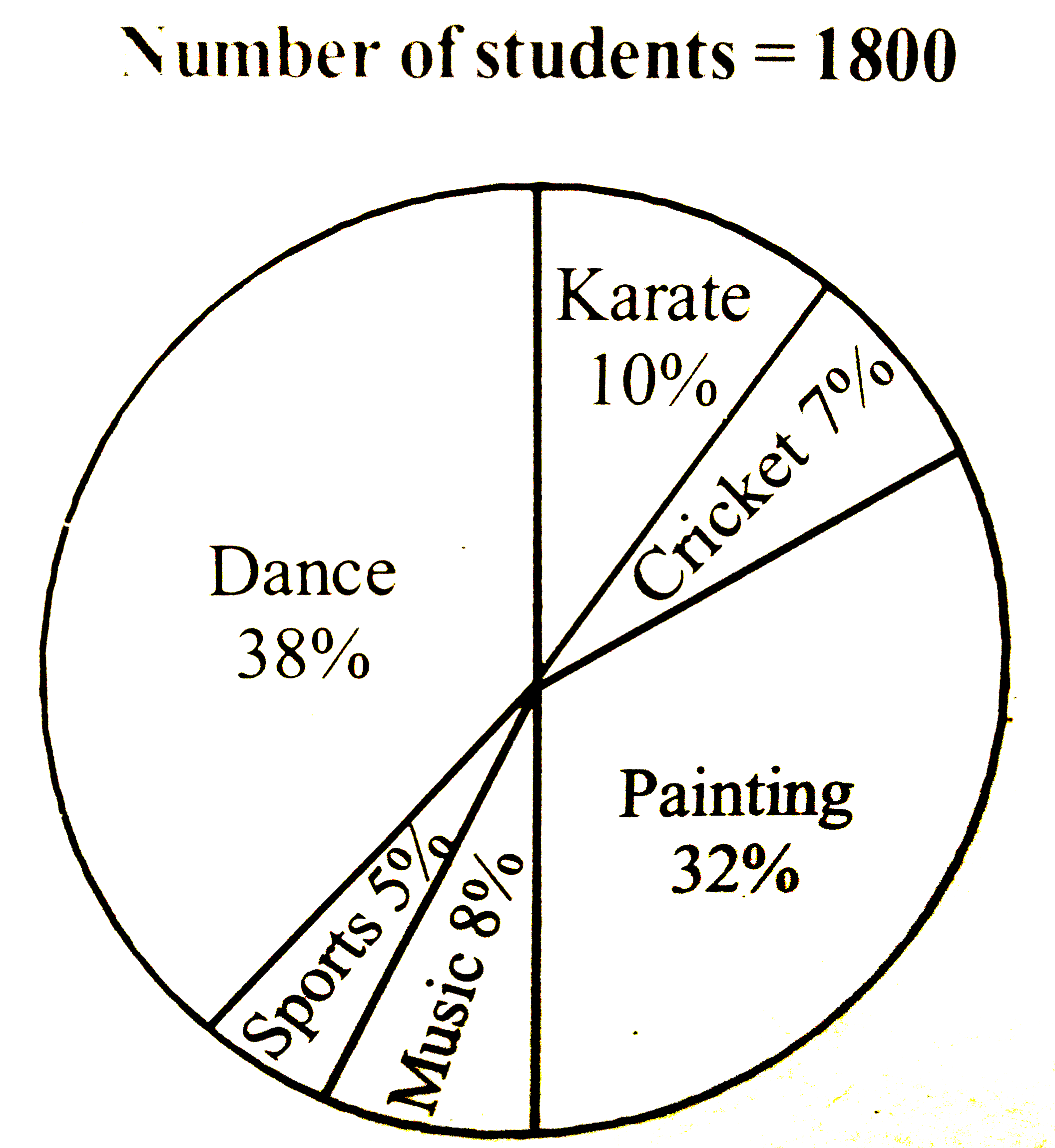
What is the respective ratio between the number of students who opted for painting and that who opted for Karate ?
View Solution
Find the average number of students who opted for Maths, Sociology and Sanskrit together ?
View SolutionIn a class there are 55 students, the number of students studying different subjects are 23 in Mathematics, 24 in Physics, 19 in Chemistry, 12 in Mathematics and Chemistry, 7 in Physics and Chemistry and 4 in all the three subjects. then the number of students who have taken exactly one subject is:
View Solution
