(a)Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid.
(b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor ?Solution in Gujrati
(a) Consider a solenoid (or an inductor) of cross-sectional area A, length l, volume V = Al and self inductance L. Suppose current passing through it at time t is I and rate of increase of current is dIdt. At this instant, if magnitude of self induced emf across the inductor is ε then we have,
ε=LdIdt
Now, if electrical power in the inductor is P then
P=εI
∴P=(LdIdt)I
∴Pdt=LIdI
∴dW=LIdI
Above is the work to be done against self induced emf to increase the current by amount dl. This work done gets stored in the magnetic field inside the solenoid in the form of magnetostatic potential energy dUB. Thus, dUB=LIdI
If current through the solenoid is increased from 0 to I in time interval from 0 to t then if total magnetostatic potential energy stored in the solenoid is UB then,
∫U0_BdUB=L∫I0IdI
∴{UB}U0_B=L{I22}I0
∴UB=12LI2...(1)
Now , magnetic field inside the solenoid, is
B=μ0nI=μ0(Nl)I
∴I=Blμ0N...(2)
Self inductance of a solenoid is given by
L=μ0N2Al ...(3)
(where N=total no. of turns in a solenoid)
From equations (1),(2)and (3)
UB=12(μ0N2Al)(B2l2μ20N2)
=12Bμ0(Al)
∴UB=12B2μ0(V)....(4) (where V=Al=volume of solenoid)
Above equation gives required expression of total magnetostatic potential energy (or magneic energy ) stored in the magnetic field , inside a current carrying solenoid having volume V.
(b)Magnetostatic potential energy stored in a solenoid (or inductor ) per unit volume is called magnetostatic potential energy density , shown by symbol ρB. Thus,
ρB=UBV...(5)
∴ρB=B22μ0
Above equation is analogous to equation or electrostatic potential energy density ρ1 (or UE) given as,
ρE=12∈0E2...(6)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section B (Numerical) Numerical From Textual Exercise
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section B (Numerical) Numerical From DARPAN Based on Textbook
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section A HOTS
2 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
14 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
Similar Questions
Predict the direction of induced current in the situations described by the following figures (a) to (d).

View SolutionA conducting circular loop is placed in a uniform magnetic field of 0.04 T with its plane perpendicular to the field. Some how, the radius of the loop starts shrinking at a constant rate of 2 mm/s. Find the induced emf in the loop at an instant when the radius becomes 2 cm solution.
View SolutionGive the explanation of reason behind the origin of motional induced emf.
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.
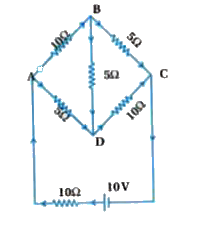
View SolutionObtain an expression for magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solonoid. (b) How does this magnetic energy compare with the elecrostatic energy strored in a capacitor ?
View SolutionWhat is expression for magnetic energy stored in an inductor. Compare it with the electrostatic energy stored in a capacitor.
View Solution(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
View Solutionएक परिनालिका, जिसमें धारा | प्रवाहित हो रही है, में संचित चुंबकीय ऊर्जा हेतु चुंबकीय क्षेत्र B, अनुप्रस्थ काट के क्षेत्रफल 4 एवं लंबाई । के पदों में व्यंजक प्राप्त कीजिए।
(b) प्रति एकांक आयतन में इस चुंबकीय ऊर्जा की तुलना समांतर प्लेट संधारित्र में प्रति एकांक आयतन में संचित स्थिर वैद्युत ऊर्जा से तुलना कीजिए।
View SolutionObtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid.
View SolutionHow does the magnetic energy compare with the electrostatic energy stored in a capacitor?
View SolutionObtain the expression for the magnetic energy stored in a coil (solenoid).
View Solutiona. Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid.
b. How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
View Solution(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
View Solution(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
View Solution
