Question

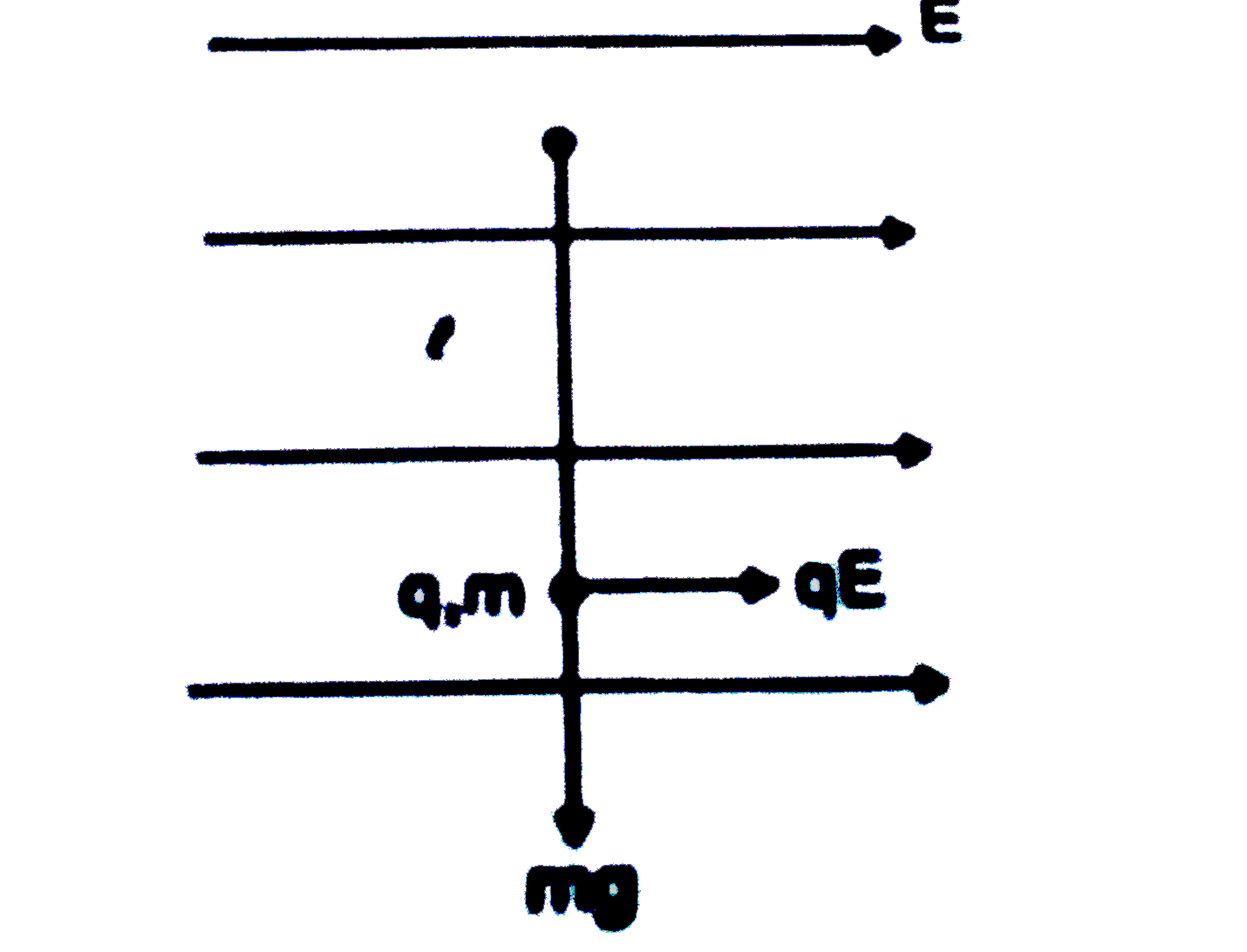
The bob of a simple pendulum of length /has a positive charge q on it. The pendulum is fixed to a horizontally oriented positively charged sheet as shown in the figure. The time period of the small oscillations of simple pendulum is

Options

A. `Equal to2pi(l/g)^(1/2)`
B. Less than `2pi(l/g)^(1/2)`
C. Greater than `2pi(l/g)^(1/2)`
D. Infinite

Explanation

To find the time period of small oscillations of a simple pendulum with a positively charged bob near a positively charged sheet, we can follow these steps:

Step 1: Understand the System
The pendulum consists of a bob of mass \( m \) and length \( L \), which has a positive charge \( q \). It is suspended above a positively charged infinite sheet. The electric field \( E \) generated by the charged sheet will affect the motion of the pendulum.

Step 2: Calculate the Electric Field
The electric field \( E \) due to an infinite sheet with surface charge density \( \sigma \) is given by:
\( E = \frac{\sigma}{2 \epsilon_0} \)
where \( \epsilon_0 \) is the permittivity of free space.

Step 3: Determine the Effective Gravity
The effective gravitational force acting on the pendulum bob will be modified due to the electric field. The effective gravitational acceleration \( g_{\text{eff}} \) can be expressed as:
\( g_{\text{eff}} = g + a \)
where \( g \) is the acceleration due to gravity, and \( a \) is the acceleration due to the electric field, which can be calculated as:
\( a = \frac{qE}{m} \)
Thus, we can write:
\( g_{\text{eff}} = g + \frac{qE}{m} \)

Step 4: Substitute the Electric Field
Substituting the expression for \( E \) into the equation for \( g_{\text{eff}} \):
\( g_{\text{eff}} = g + \frac{q}{m} \cdot \frac{\sigma}{2 \epsilon_0} \)

Step 5: Write the Formula for Time Period
The time period \( T \) of a simple pendulum is given by:
\( T = 2\pi \sqrt{\frac{L}{g_{\text{eff}}}} \)
Substituting the expression for \( g_{\text{eff}} \):
\( T = 2\pi \sqrt{\frac{L}{g + \frac{q\sigma}{2m\epsilon_0}}} \)

Step 6: Analyze the Result
The time period \( T \) is affected by the additional term due to the electric field. As the electric field increases, the effective gravitational force increases, which in turn decreases the time period of the pendulum.

Final Expression
Thus, the final expression for the time period of the small oscillations of the pendulum is:
\( T = 2\pi \sqrt{\frac{L}{g + \frac{q\sigma}{2m\epsilon_0}}} \)