Two identical capacitors of plate dimensions l×b and plate separation 'd' have dielectric slabs filled in between the space of the plates as shown in Fig
Obtain the relation between the dielectric constants K,K1 and K2.
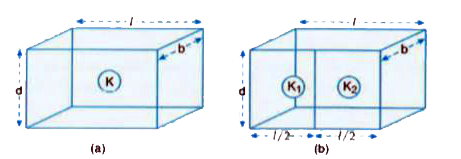
For capacitor shown in fig area of each plate of capacitor A1=lb and capacitance C1=K∈0A1d
The capacitor shown in Fig is equivalent to two capacitors each of plate area A2=l2.b=lb2=A12 but filled with dielectrics of dielectric constants K1 and K2 respectively joined in series . Therefore , net capacitance of this arrangement is
C2=K1∈0(A1/2)d+K2∈0(A1/2)d=∈0A1d[K1+K22]
Since C1=C2 hence we conclude that K∈0A1d=∈0A1d[K1+K22]⇒K=K1+K22
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-I
64 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
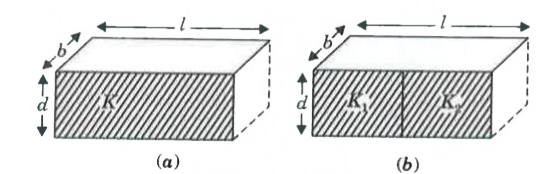
Two identical capacitors of plate dimensions: l×b and plate separation d have dielectric slabs filled in between the space of the plates as shown in the figures. if capacitance of both capacitor is same, Obtain the relation between the dielectric constant K,K1andK2.
View SolutionFigure shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dieletric constant K is placed in between the plates of the capacitor as shown.

The electric field in the gaps between the plates and the electric slab will be
View Solution
Knowledge Check
Figure shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dieletric constant K is placed in between the plates of the capacitor as shown.

The electric field in the gaps between the plates and the electric slab will beAε0AVdBVdCKVdDVd−tFigure shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dielectric constant K is placed in between the plates of the capacitor as shown.

The electric field in the dielectric slab isAVKdBKVdCVdDKVtCapacitance of a capacitor becomes 76 times of its original value if a dielectric slab of thickess t=24d is introduced in between the plates, d is the separation between the plates. The dielectric constant of the dielectric slab is
A1411B1114C711D117
Two identical parallel plate (air) capacitors c1andc2 have capacitances C each. The space between their plates is now filled with dielectrics as shown. If two capacitors still have equal capacitance, obtain the relation betweenn dielectric constants k,k1andk2.
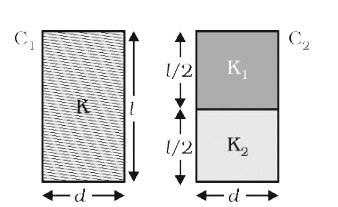
View SolutionTwo identical parallel plate (air) capacitors c1andc2 have capacitances C each. The space between their plates is now filled with dielectrics as shown. If two capacitors still have equal capacitance, obtain the relation betweenn dielectric constants k,k1andk2.

View SolutionFigue shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dieletric constant K is placed in between the plates of the capacitor as shown.

The electric field in the dielectric slab is
View SolutionTwo dielectric slabs of constant K1 and K2 have been filled in between the plates of a capacitor as shown below. What will be the capacitance of the capacitor
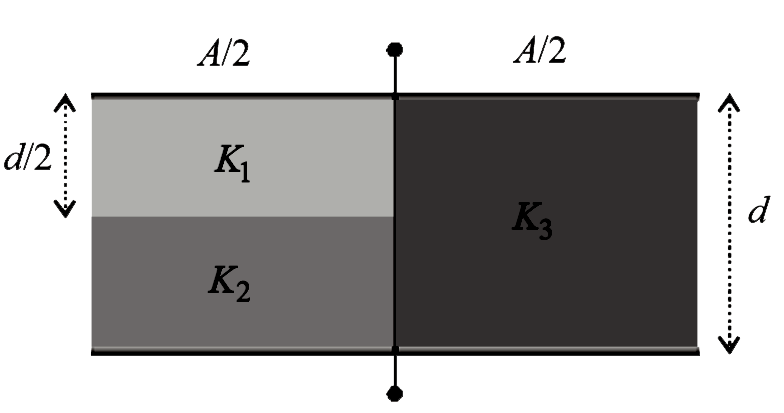
View SolutionA parallel plate capacitor with air between the plates has a capacitance of 9 pF. The separation between its plates is ‘d'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant K1=3 and thickness d3 while the other one has dielectric constant K2=6 and thickness 23d. Capacitance of the capacitor is now
View Solution
