(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30°. Calculate the speed of light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.

(i) Here angle of prism A = 60° and angle of minimum deviation Dm=30∘ ,
∴ Refractive index of prim n=sin(A+Dm)2sin(A2)=sin(60∘+30∘)2sin(60∘2)=sin45∘sin30∘1√2/12=√2
∴ speed of light through the prism v=cn=3×108√2=2.12×108ms−1
As the emergent ray grazes along the face AC, hence ∠r2 at face AC must be equal to critical angle ic. Thus,
r2=ic=sin−1(1n)=sin−1(1√2)=45∘⇒r1=A−r2=60∘−45∘=15∘
If angle of incidence at the face AB be i, then sinisinr=n
⇒sini=nsinr1=√2×sin15∘=√2×0.2588=0.3660⇒i=sin−1(0.3660)=21.5∘
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - LONG ANSWER QUESTIONS-II
9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SELF ASSESSMENT TEST (SECTION A)(MULTIPLE CHOICE QUESTIONS)
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SHORT ANSWER QUESTIONS
54 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - U-LIKE SERIESCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - SECTION B
1 Videos
Similar Questions
A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 306∘ .Calculate the speed of light through the prism.
View SolutionIn the above example, find the angle of incidence at face AB, so that emergent ray grazes along the face AC'.
View Solution(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30∘. Calculate the speed of the light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
View SolutionAnswer the following:
(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30∘. Calculate the speed of the light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.

View SolutionIn the above example, find the angle of incidence at face AB, so that emergent ray grazes along the face AC'.
View SolutionA ray of incident on an equilateral prism shows minimum deviation of 30∘ .The speed of light through the prism is ?
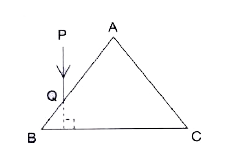
View SolutionA ray of light PQ is incident on the face AB of an equilateral glass prism ABC as shown in the figure. Show that angle of emergence = angle of deviation. Also, with a ray diagram, trace the path of the emergent ray.
View SolutionA light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionAt what angle, a ray of light should be incident on the first face AB of a regular glass prism ABC so that the emergent ray grazes the adjacent face AC ?

View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges.
View Solution
