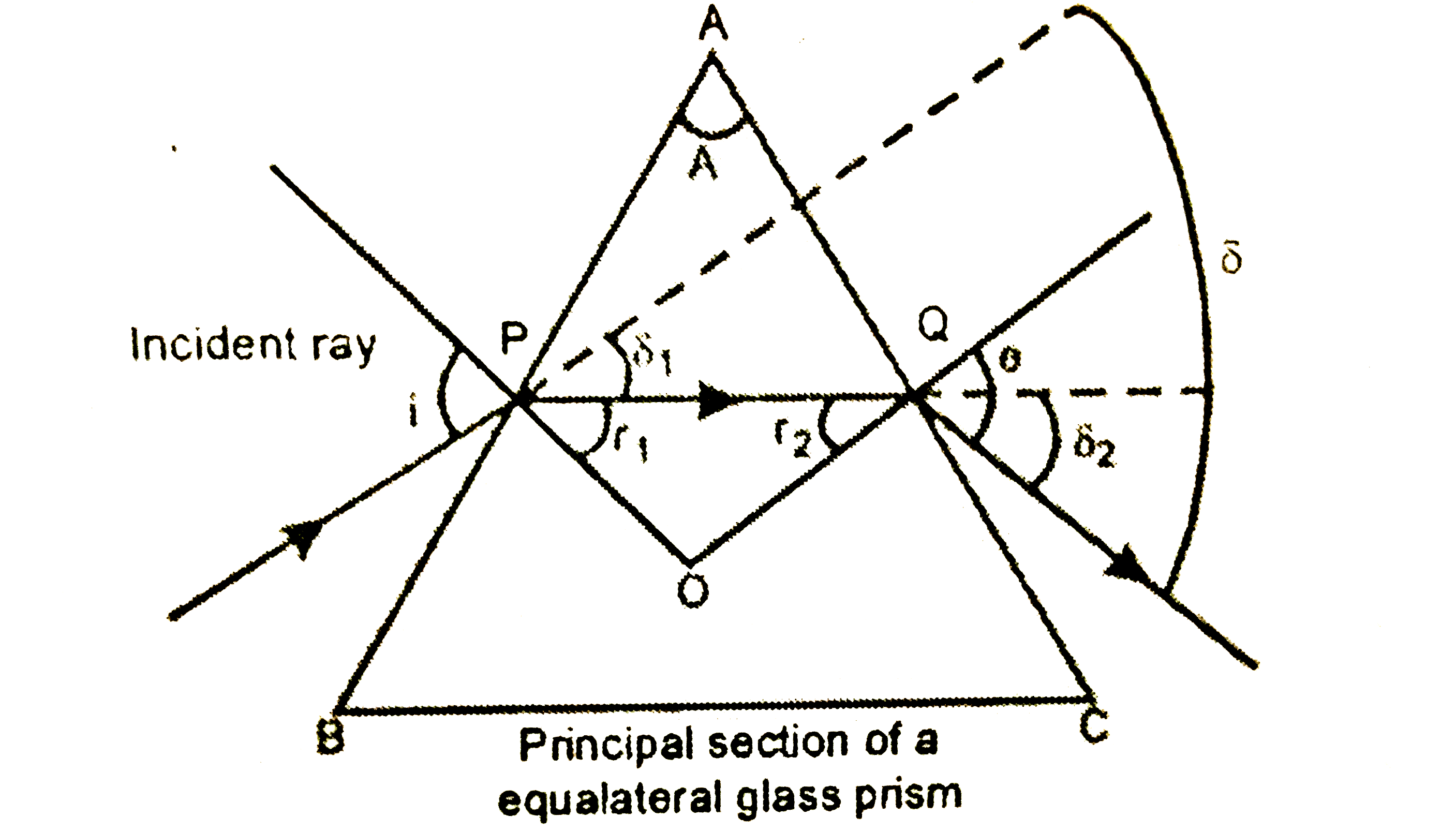
A ray 'PQ' of light is incident on the face AB of a glass prism ABC [Fig. 9.86] and emerges out of the face AC. Trace the path of the ray. Show that
∠i+∠e=∠A+∠B
where δ and e where 8 and e denote the angle of deviation and angle of emergence respectively.
(b) Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. State the condition under which ∠δ is minimum.
(c) Find out the relation between the refractive index ∠A of the glass prism and ∠A for the case when the angle of prism (A) is equal to the angle of minimum deviation (δm). Hence, obtain the value of the refractive index for angle of prism A = 60°.
![A ray 'PQ' of light is incident on the face AB of a glass prism ABC [Fig. 9.86] and emerges out of the face AC. Trace the path of the ray. Show that anglei + anglee = angleA + angleB where delta and e where 8 and e denote the angle of deviation and angle of emergence respectively. (b) Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. State the condition under which angledelta is minimum. (c) Find out the relation between the refractive index angleA of the glass prism and angleA for the case when the angle of prism (A) is equal to the angle of minimum deviation (delta(m)). Hence, obtain the value of the refractive index for angle of prism A = 60°.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/U_LIK_SP_PHY_XII_C09_E10_002_Q01.png)
Refraction of light rays through a prism has been shown in Fig. 9.87. Here ∠i is the incidence angle at first surface of prism and ∠r1 is the angle of emergence from the second surface. ∠r1 and ∠r2 are the respective refraction angles at the two faces and ∠δ is the angle of deviation.
Now, in ΔQMR,∠r1+∠r2+∠M=180∘ ...............(i)
and in quadrilateral AQMR, ∠A=90∘+∠M+90∘=360∘
∠A+∠M=180∘......(ii)

Comparing (i) and (ii), we get
∠r1+∠r2=∠A
Now, in △JQR,∠JRQ
=(∠i−∠1)(∠e−∠r2)=∠i+∠e−(∠r1+∠r2)=∠i+∠e−∠A
⇒∠i+∠=∠A+∠B
(b) A graph showing variation in angle of deviation (δ) with variation in angle of incidence (z) is shown below. As minimum deviation position corresponds to only one angle of incidence, it means that for minimum deviation position ∠i=∠e and also ∠r1=∠r2=r (say).
(c) In minimum deviation position
∠A=∠r1+∠r2=∠r+∠r=2√r or ∠r=(A2)
and ∠A+∠δm=∠i+∠e=∠i+∠i=2∠i or ∠i=A+δm2
∴ Refractive index of prism n=sinisinr=sin(A+δm)2sin(A2)
If δm=A
=sinAsinA/2=2sinA2.cosA2sinA2=2cosA2
If angle of prism ∠A=60∘, them
Refractive index n=2cos(60∘2)=2cos30∘=2×√32=√3
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:U-LIKE SERIESChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:SELF ASSESSMENT TEST (SECTION A)(MULTIPLE CHOICE QUESTIONS)
Explore 5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:U-LIKE SERIESChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:SELF ASSESSMENT TEST (SECTION A)(FILL IN THE BLANKS)
Explore 3 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:U-LIKE SERIESChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:LONG ANSWER QUESTIONS-I
Explore 38 Videos
- NUCLEIBook:U-LIKE SERIESChapter:NUCLEIExercise:Self Assessment Test
Explore 10 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:U-LIKE SERIESChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:SECTION B
Explore 1 Video
Similar Questions
Consider two coherent sources S1andS2 producing monochromatic waves to produce interference patten. Let the displacement of the wave produced by S1 be given by
and the displacement by S2 be Y1=acosωt
Y2=acos(ωt−ϕ)
Find out expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be
I=4a2cos2ϕ/2
Hence establish the conditions for constructive and destructive interference.
(b) What is the effect on the interference friinges in Young's double slit experiment when (i) the width of the source slit is increased, (ii) the monochromatic source is replaced by a source is replaced by a source of white light ?
OR
(a) A ray, 'PQ' of light on the face AB of glass prism ABC (as shown in the figure) and emerges out of the face AC. Trace the path of the ray. Show that
∠i+∠e=∠A+∠δ
Where δ and e denote the angle of deviation and angle of emergence respectively.
Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. state the condition under which ∠δ is minimum.
(b) Find out the relation between the refractive index (μ) of the glass prism and ∠A for the case when the angle of prism (A) is equal to the angle of minimum deviation (δm) . Hence obtain the value of the refractive index for angle Ae=60∘ .
View SolutionA ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View Solution
Knowledge Check
A ray of light is incident on one face of a prism at an angle of 50∘ with the normal . The ray is deviated by the prism through 42∘ . What is the angle of the prism , if the angle of emergence is 51∘ ?
A56∘B57∘C58∘D59∘A ray of light is incident on one of the faces of the angle prism with an angle 40∘ with the surface. The angle of the prism is 60∘. The emergent ray is deviated through an angle 38∘. The angle of emergence is
A38∘B48∘C52∘D58∘
A ray of light PQ is incident on the face AB of an equilateral glass prism ABC as shown in the figure. Show that angle of emergence = angle of deviation. Also, with a ray diagram, trace the path of the emergent ray.
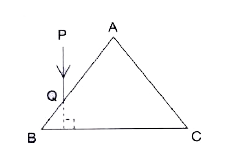
View SolutionAt what angle, a ray of light should be incident on the first face AB of a regular glass prism ABC so that the emergent ray grazes the adjacent face AC ?

View SolutionA ray of light is incident on one face of prism making an angle of 50∘ with the face. If emergent ray from the prism is made to retrace its path, what would be the angle of emergence ?
View SolutionA ray of light is incident on the face AB of a glass prism ABC having vertex anlge A equal to 30∘. The face AC is silvered and a ray of light incident on the face AB retraces its path. If the refractive index of the material of prism is √3 find the angle of incidence on the face AB.
View SolutionThe angle between the incident ray and the emergent ray in a glass prism is called (angle of incidence/angle of deviation).
View SolutionA ray of light is incident on one of the faces of the angle prism with an angle 40∘ with the surface. The angle of the prism is 60∘. The emergent ray is deviated through an angle 38∘. The angle of emergence is
View Solution
