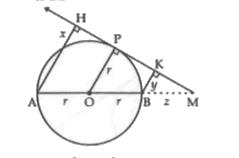
AB is a diameter of circle. P is a point on the semicircle APB. AH and BK are perpendiculars from A and B respectively to the tangents at P. Prove that AH+BK=AB.
 Solution in Kannada
Solution in Kannada
Step by step video & image solution for AB is a diameter of circle. P is a point on the semicircle APB. AH and BK are perpendiculars from A and B respectively to the tangents at P. Prove that AH+BK=AB. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS)
2 Videos
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)
9 Videos
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( SHORT ANSWER [SA] TYPE - 2 - QUESTIONS)
13 Videos
- ARITHMETIC PROGRESSIONSBOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - ZEN ADDITIONAL QUESTIONS (HOTS [HIGHER ORDER THINKING SKILLS] - QUESTIONS)
4 Videos
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - HIGHER ORDER THINKING SKILLS [HOTS] QUESTIONS
14 Videos
Similar Questions
If a, b, and c, are the sides of a right-angled triangle where C is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by r=a+b−c2 units.
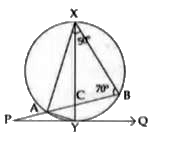
View SolutionIn the adjoining figure, XY is a diameter of the circle and PQ is a tangent to the circle at Y. Given that ⌊AXB=50∘ and ⌊ABX=70∘, calculate ⌊BAY and ⌊APY.
View SolutionProve that "the lengths of tangents drawn from an external points to a circle are equal ".
View SolutionIf m times the mth term of an A.P. is equal ton times the nth term and m≠n, show that (m+n)th term is zero.
View SolutionIn what ratio does 4x +3y-13 0 divide the line segment joining (2, 1) and (1, 4)?
View SolutionAB is a diameter of a circle. P is a point on the semi-circle APB.AHandBK are perpendiculars from AandB respectively to the tangent at P. Prove that AH+BK=AB.
View SolutionAB is a diameter of a circle.AH and BK are perpendiculars from A and B respectively to the tangent at P Prove that AH+BK=AB .
View SolutionIn the given figure (not to scale), O is the centre of the circle. A,B,C and D are concyclic and AB=CD . If /_MON =120^(@) , then find /_ OPN .
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solution
