AB एक वृत्त का एक व्यास है । अर्धवृत्त APB पर P एक बिंदु है| P से गुजरने वाली स्पर्श रेखा पर A तथा B एक लम्ब क्रमशः AH तथा BK हैं| सिद्ध करें कि AH+BK=AB है|
स्पष्ट है कि ∠MPO=90∘
चूँकि BK⊥HM,AH⊥HM तथा OP⊥HM है । अतः
AH||OP||∣BK
माना AH=x,BK=y तथा OP=r पुनः मान लें ,BM =z
अब ,ΔMKB तथा ΔMHA में हम देखते हैं कि,
∠MKS=∠MHA=90∘
तथा ∠BMK=∠AMH " " [ उभयनिष्ट ]

अतः AA समरूपता अभिगृहित से
ΔMKB~ΔMHA
⇒BKAH=MBMA
⇒yx=z2r+z⇒2ry+yx=zx⇒z=2ryx−y ... (i)
अब ΔMKS तथा ΔMPO में , हम देखते है कि ∠MKB=∠MPO=90∘
∠BMK=∠OMP
अतः AA समरूपता अभिगृहित से,
ΔMKB~ΔMPO
⇒BKOP=BMOM
⇒yr=zr+z
⇒ry+yz=rz
⇒z=ryr−y ... (ii)
अब (i) तथा (ii) से
ryr−y=2ryx−y
⇒2r−2y=x−y
⇒2r−x+y
⇒AB=AH+BK
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.14videos
वृत्त
- BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.222videos
वृत्त
- BOOK - RD SHARMACHAPTER - वास्तविक संख्याएँ EXERCISE - बहु विकल्पीय प्रश्न25videos
वास्तविक संख्याएँ
- BOOK - RD SHARMACHAPTER - वृत्तों से सम्बन्धित क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न45videos
वृत्तों से सम्बन्धित क्षेत्रफल
Similar Questions
रिक्त स्थानों की पूर्ति कीजिए :
(i) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को कहते ………. हैं।
(ii) एक वृत्त की ..... समानान्तर स्पर्श रेखाएँ हो सकती हैं ।
(iii) किसी वृत्त की स्पर्श रेखा उसे ..... बिंदुओं पर प्रतिच्छेद करती है ।
(iv) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को कहते हैं ।
(v) वृत्त पर स्पर्श रेखा के स्पर्श बिन्दु तथा उस बिन्दु से गुजरने वाली त्रिज्या के बीच का कोण ...... का होता है ।03:29View Solutionयदि किसी वृत्त C(O,r) पर PT स्पर्श रेखा है तथा OP=17 सेमी और OT =8 सेमी हो , तो स्पर्श रेखा की लम्बाई ज्ञात करो ।
01:04View Solution144 के अभाज्य गुणनखण्डों में 2 की घात है :
00:59View Solutionएक वृत्त की परिधि तथा क्षेत्रफल रूप से समान हों, तो वृत्त का व्यास है :
01:41View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
07:40View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
04:26View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
06:39View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
07:31View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
05:20View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
03:52View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
02:16View SolutionAB is a diameter of circle. P is a point on the semicircle APB. AH and BK are perpendiculars from A and B respectively to the tangents at P. Prove that AH+BK=AB.
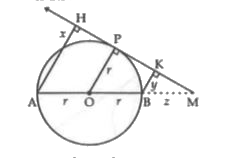 03:18View Solution
03:18View SolutionAB is a diameter of a circle with centre O. CB is a tangent to the circle at B. AC intersects the circle at G. If the radius of the circle is 6cm and AG = 8cm, then the length of BC is : AB एक वृत्त का व्यास है जिसका केंद्र O है | CB, B पर वृत्त की स्पर्श रेखा है| AC, वृत्त को G पर काटता है | यदि वृत्त की त्रिज्या 6 सेमी है तथा AG = 8 सेमी है, तो BC की लंबाई ज्ञात करें |
04:10View SolutionIn a circle with centre O, PQR is a tangent at the point Q on it. AB is a chord in the circle parallel to the tangent such that angle BQR= 70^@ . What is the measure of angle AQB ? केंद्र O वाले एक वत्त में, PQR इस पर स्थित बिंदु Q पर एक स्पर्श रेखा है | AB वृत्त में एक जीवा है जो स्पर्श रेखा से इस प्रकार समानांतर है कि angle BQR= 70^@ है | angle AQB का मान ज्ञात करें |
07:19View SolutionFrom a point P , outside a circle, PAB is a secant and PT is a tangent to the circle, where A , B and T are points on the circle. If PT = 5cm , PA = 4cm and AB = x , then x is equal to: वृत्त के बाहर एक बिंदु P से , PAB एक छेदक रेखा तथा PT वृत्त की एक स्पर्श रेखा है एवं A, B और T वृत्त पर स्थित बिंदु हैं | यदि PT=5 सेमी, PA = 4 सेमी तथा AB = x सेमी है, तो x का मान किसके बराबर होगा ?
04:08View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle, and A and B are points on the circle. If angle APB= 40^@ , then angle OAB is equal to: PA तथा PB एक वृत्त के बाहर स्थित बिंदु P से वृत्त की स्पर्श रेखाएं हैं जिसका केंद्र O है तथा A और B वृत्त पर स्थित बिंदु हैं | यदि angle APB= 40^@ है, तो angle OAB का मान ज्ञात करें |
03:15View Solution

