Using Division Algorithm prove that the polynomial g(x)=x2+3x+1 is a factor of f(x)=3x4+5x3−7x2+2x+2 Solution in Kannada
The correct Answer is:i.e., g (x) is a factor of f(x)
Step by step video, text & image solution for Using Division Algorithm prove that the polynomial g(x) = x^(2) + 3x + 1 is a factor of f(x) = 3 x^(4) + 5 x^(3) - 7 x^(2) + 2x + 2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- POLYNOMIALSBook:ZEN PUBLICATIONChapter:POLYNOMIALSExercise:TEXTUAL EXERCISE ( Exercise 9 . 1 )
Explore 1 Video
- POLYNOMIALSBook:ZEN PUBLICATIONChapter:POLYNOMIALSExercise:TEXTUAL EXERCISE ( Exercise 9 . 2 )
Explore 2 Videos
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBook:ZEN PUBLICATIONChapter:PAIR OF LINEAR EQUATIONS IN TWO VARIABLESExercise:ADDITIONAL QUESTIONS - HIGHER ORDER THINKING SKILLS (HOTS)
Explore 12 Videos
- PROBABILITYBook:ZEN PUBLICATIONChapter:PROBABILITYExercise:ZEN ADDITIONAL QUESTIONS HOTS [HIGHER ORDER THINKING SKILLS]-QUESTIONS
Explore 24 Videos
Similar Questions
(i) The graphs of y p(x) are given in Fig. below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
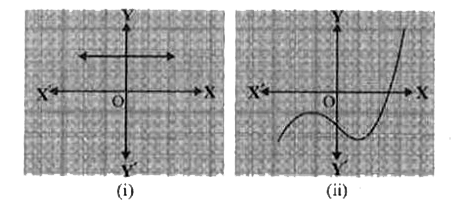
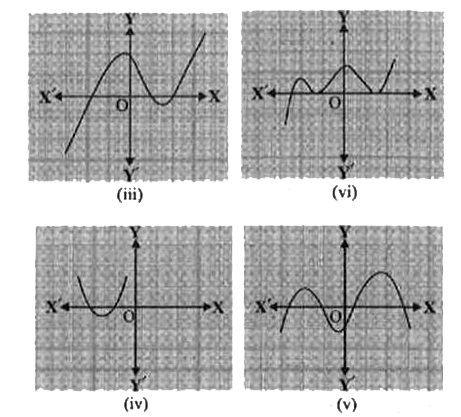
View SolutionFind the zeroes of the following quadratic polynomials and varify the relationship between the zeroes and the coefficients.
t2−25
View SolutionSolve for x and y in the following question :
2x+2y+12x−y+59=0,9x+2y+62x−y+4=0
View SolutionA number x is chosen at random from numbers -3,-2,-1,0,1,2, and 3. find the probability that |x|<2.
View SolutionDivide the polynomial f(x)=3x2−x3−3x+5 by the polynomial g(x)=x-1and verify the division algorithm.
View SolutionBy applying division algorithm prove that the polynomial g(x)=x2+3x+1 is a factor of the polynomial f(x)=3x4+5x3−7x2=2x=2.
View SolutionBy applying division algorithm prove that the polynomial g(x)=x2+3x+1 is a factor of the polynomial f(x)=3x4+5x3−7x2+2x+2.
View Solutionबहुपद f(x)=3x2−x3−3x+5 को बहुपद g(x)=x−1−x2 से भाग दीजिए और विभाजन एल्गोरिथ्म को सत्यापित कीजिए।
View Solutionविभाजन एल्गोरिथम का प्रयोग करते हुए जाँच करे कि बहुपद x3−3x+1, बहुपद x5−4x3+x2+3x+1 का एक गुणनखण्ड है या नहीं |
View Solutionइनमें बहुपद f(x) को बहुपद g(x) के द्वारा विभाजित कर भागफल और शेषफल ज्ञात करने के लिए विभाजन एल्गोरिथ्म का प्रयोग कीजिये |
f(x)=x3−3x2+5x−3,g(x)=x2−2
View Solutionविभाजन एल्गोरिथ्म का प्रयोग करके सिद्ध कीजिये कि बहुपद g(x)=x2+3x+1 बहुपद f(x)=3x4+5x3−7x2+2x+2 का एक गुणनखण्ड है |
View Solutionगुणनखंड प्रमेय का प्रयोग करके जाँचिये की g(x), बहुपद f(x) का गुणनखंड है या नहीं।
(i) f(x)=x3−6x2−19x+84, g(x)=x−7
(ii) f(x)=x3−3x2+4x−4, g(x)=x−2
(iii) f(x)=3x4+17x3+9x2−7x−10, g(x)=x+5
(iv) f(x)=2x3+4x+6, g(x)=x+1
View SolutionDivide the polynomial g(x)=x3−3x2+x+2 by the polynomial x2−2x+1 and verify the division algorithm.
View Solutionविभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p (x ) को g (x ) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए :
p(x)=3x3−x2+2x+5,g(x)=1+2x+x2
View SolutionDivide the polynomial g(x)=x3−3x2+x+2 by the polynomial x2−2x+1 and verify the division algorithm.
View Solution