The value of the mode when mean is 146 and median is 130 is Solution in Kannada
276
108
98
138
The correct Answer is:C
Step by step video, text & image solution for The value of the mode when mean is 146 and median is 130 is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STATISTICS BOOK - ZEN PUBLICATIONCHAPTER - STATISTICS EXERCISE - ZEN ADDITIONAL QUESTIONS (VERY SHORT ANSWER [VSA] TYPE QUESTIONS)
10 Videos
- STATISTICS BOOK - ZEN PUBLICATIONCHAPTER - STATISTICS EXERCISE - ZEN ADDITIONAL QUESTIONS (SHORT ANSWER [SA] TYPE I QUESTIONS)
9 Videos
- STATISTICS BOOK - ZEN PUBLICATIONCHAPTER - STATISTICS EXERCISE - TEXTUAL EXERCISES (Exercise 13.4)
3 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - ZEN PUBLICATIONCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - ADDITIONAL QUESTIONS (VALUE BASED QUESTIONS )
2 Videos
- SURFACE AREAS AND VOLUMESBOOK - ZEN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - ZEE ADDITIONAL QUESTIONS -HOTS [HIGHER ORDER THINKING SKILLS]-QUESTIONS
11 Videos
Similar Questions
Write the class mark of the class x-y.
View SolutionFind the mean of the distribution.

View SolutionThe following distribution gives the daily income of 50 workers of a factory.
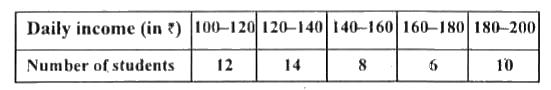
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
View SolutionThe angle of elevation of the top of a chimney from the foot of a tower is 60∘ and the angle of depression of the foot of the chimney from the top of the tower is 30∘. If the height of the tower is 40m, find the height of the chimney. According to pollution control norms, the minimum height of a smoke-emitting chimney should be 100m. State if the height of the above mentioned chimney meets the pollution control norms. What value is discussed in this question?
View SolutionA sector of a circular is of radius 12 cm and angle 120∘. It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone.
View SolutionFind the value of mean,median and mode for the following: 36,32,28,22,26,22,18,40
View SolutionIf mean =(3 median-mode) x then value of x is
View SolutionOne of the methods of determining mode is (a) Mode = 2 Median – 3 Mean (b) Mode = 2 Median + 3 Mean (c) Mode = 3 Median – 2 Mean (d) Mode = 3 Median + 2 Mean
View SolutionCalculate mode when arithmetic mean is 146 and median is 130.
View Solutioni. Mean = a (3 median - mode)
II. Mean - Mode = b(Mean - Median)
(iii) Median = Mode + c (Mean - mode)
View SolutionFor a frequency distribution, mean, median and mode are connected by the relation (a) Mode = 3 Mean – 2 median (b) Mode = 2 Median – 3 Mean (c) Mode = 3 Median – 2 Mean (d) Mode = 3 Median + 2 Mean
View SolutionOne of the methods of determining mode is (a) Mode = 2 Median – 3 Mean (b) Mode = 2 Median + 3 Mean (c) Mode = 3 Median – 2 Mean (d) Mode = 3 Median + 2 Mean
View SolutionMode -Mean=….(Median-Mean)
View SolutionIf Mode= 18 and Median = 21, find the value of Mean
View SolutionFind the mean when median is 72.5 and mode is 70.
View Solution
