For a frequency distribution, mean, median and mode are connected by the relation (a) Mode = 3 Mean – 2 median (b) Mode = 2 Median – 3 Mean (c) Mode = 3 Median – 2 Mean (d) Mode = 3 Median + 2 Mean
To solve the question regarding the relationship between mean, median, and mode in a frequency distribution, we will analyze the provided options and determine which one is correct.
1. Understanding the Relationship:
The relationship between mean, median, and mode is often expressed in terms of a specific formula. The most common formula that connects these three measures of central tendency is:
Mode=3×Median−2×Mean
This formula is particularly valid for symmetrical distributions and moderately skewed distributions.
2. Analyzing the Options:
We need to check each option against the known relationship:
- (a) Mode = 3 Mean – 2 Median
- (b) Mode = 2 Median – 3 Mean
- (c) Mode = 3 Median – 2 Mean
- (d) Mode = 3 Median + 2 Mean
3. Identifying the Correct Option:
From our understanding, the correct relationship is:
Mode=3×Median−2×Mean
This matches option (c).
4. Conclusion:
Therefore, the correct answer is:
(c) Mode = 3 Median - 2 Mean
The relationship between mean, median, and mode is often expressed in terms of a specific formula. The most common formula that connects these three measures of central tendency is:
Mode=3×Median−2×Mean
This formula is particularly valid for symmetrical distributions and moderately skewed distributions.
We need to check each option against the known relationship:
- (a) Mode = 3 Mean – 2 Median
- (b) Mode = 2 Median – 3 Mean
- (c) Mode = 3 Median – 2 Mean
- (d) Mode = 3 Median + 2 Mean
From our understanding, the correct relationship is:
Mode=3×Median−2×Mean
This matches option (c).
Therefore, the correct answer is:
(c) Mode = 3 Median - 2 Mean
Topper's Solved these Questions
Similar Questions
One of the methods of determining mode is (a) Mode = 2 Median – 3 Mean (b) Mode = 2 Median + 3 Mean (c) Mode = 3 Median – 2 Mean (d) Mode = 3 Median + 2 Mean
View SolutionThe relationship between mean, median and mode for a moderately skewed distribution is (a) Mode = 2 Median – 3 Mean (b) Mode = Median – 2 Mean (c) Mode = 2 Median – Mean (d) Mode = 3 Median – 2 mean
View SolutionFind mean, median and mode of the following data :
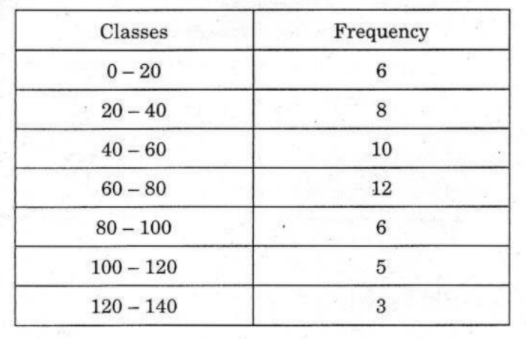
View SolutionFind the median and mode of the data:
View SolutionFind the mean, median and mode of the following data

View SolutionFind the mean, median and mode of the following data :

View Solutioni. Mean = a (3 median - mode)
II. Mean - Mode = b(Mean - Median)
(iii) Median = Mode + c (Mean - mode)
View SolutionFor a normal distribution if the mean is M, mode is M0 and median is Md, then
View SolutionIn a binomial distribution, the mean is 4 and variance is 3. Then its mode is
View SolutionIf for a moderately skewed distribution, mode = 60 and mean = 66, then median =
View Solution
