An ellipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is Solution in Telugu
1/9
4/9
1/3
2/3
The correct Answer is:D
Step by step video, text & image solution for An ellipse of eccentricity (2sqrt(2))/(3) is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - Random Variable17videos
APPENDICES (REVISION EXERCISE)
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - Statistics18videos
APPENDICES (REVISION EXERCISE)
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - Combinations20videos
APPENDICES (REVISION EXERCISE)
- BOOK - AAKASH SERIESCHAPTER - AREASEXERCISE - Exercise-3.221videos
AREAS
Similar Questions
A student has to match three historical events Dandi March, Quit India movement and Mahatma Gandhi Assassination with the years 1948,1930 and 1942. The student has no knowledge of the correct answers and decided to match the events and years randomly. If x denotes the number of correct answers he gets, then mean of x is
04:32View SolutionThe number of students absent in a class were recorded every day for 120 days and the information is given in the following frequency table. Then mean number of students absent per day is
No. of student absent01234567No. of days 14105034154203:00View SolutionmCr+1+n∑k=mkCr is equal to :
05:12View SolutionFind the area of the region bonded by y=x(x−1)(x−2), the x-axis and x = 0 and x = 4.
View SolutionAn ellipse is inscribed in a circle and a point within the circle is chosen at random. If the probability that this point lies outside the ellipse is 23 then the eccentricity of the ellipse is: (A) 2√23 (B) √53 (C) 89 (D) 23
05:30View SolutionA square is inscribed in a circle.If p_(r) is the probability that a randomly chosen point inside the circle lies within the square and p, is the probability that the point lies outside the square,then
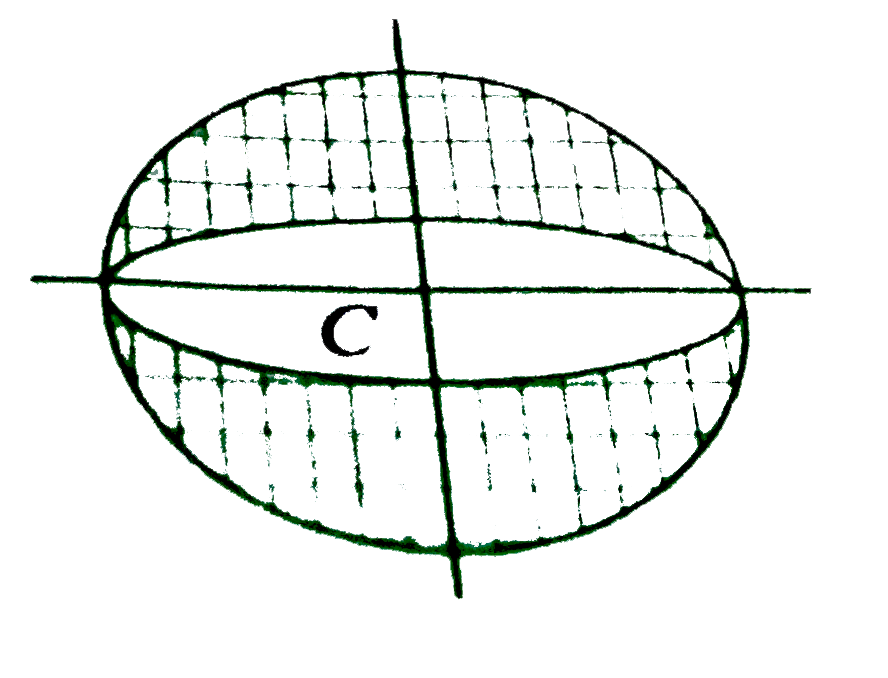
02:28View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
A point is selected at random inside a circle. The probability that the point is closer to the center of the circle than to its circumference is04:54View SolutionAn ellipse of eccentricity 2√23 is inscribed in a circle . A point is chosen inside the cirlce at random. The probaboility that the point lies outside the ellipse is
02:50View SolutionA circle of maximum area is inscribed in an ellipse. If p is the probability that a point within the ellipse chosen at random lies outside the circle, then the eccentricity of the ellipse is
03:47View SolutionThe ratio of ordinates of a point on ellipse and its corresponding point on auxiliary circle is 2√23 then its eccentricity is
03:08View SolutionA square is incribed in a circle . If p_(1) is the probability that a randomly chosen point of the circle lies within the square and p_(2) is the probability that the point lies outside the square then
03:26View SolutionIf the ratio of the ordinate of a point on ellipse and its corresponding point on auxiliary circle is 2√23 then its eccentricity is
06:53View SolutionAn ellipse is inscribed in its auxiliary circle and a point within the circle is chosen at random. If p is the probability that this point lies outside the ellipse and inside the auxiliary circle. Then 8p is equal to (where eccentricity of the ellipse is √32)
(A) 3 (B) 4 (C) 6 (D) 101:30:02View SolutionAn ellipse is inscribed in its auxiliary circle and a point within the circle is chosen at random. If p is the probability that this point lies outside the ellipse and inside the auxiliary circle. Then 8p is equal to (where eccentricity of the ellipse is √32)
(A) 3 (B) 4 (C) 6 (D) 105:13View SolutionEccentricity (2sqrt(3))/3 A point is randomly selected under an ellipse of a circle. The point is that the probability that the ellipse will be located outside is
04:44View SolutionAn ellipse of eccentricity (2sqrt(2))/(3) is inscribed in a circle . A point is chosen inside the cirlce at random. The probaboility that the point lies outside the ellipse is
04:09View Solution