Question

A circle of maximum area is inscribed in an ellipse. If p is the probability that a point within the ellipse chosen at random lies outside the circle, then the eccentricity of the ellipse is

Options

A. `sqrt(1-p)`
B. `sqrt(1-(1-p)^(2))`
C. `sqrt(1-p^(2))`
D. `sqrt((1+p)^(2)-1)`

Answer

B

Explanation

To solve the problem step by step, we will follow the logic presented in the video transcript.

Step 1: Understand the Problem
We need to find the eccentricity of an ellipse given that a circle of maximum area is inscribed in it, and we are given the probability \( p \) that a randomly chosen point inside the ellipse lies outside the circle.

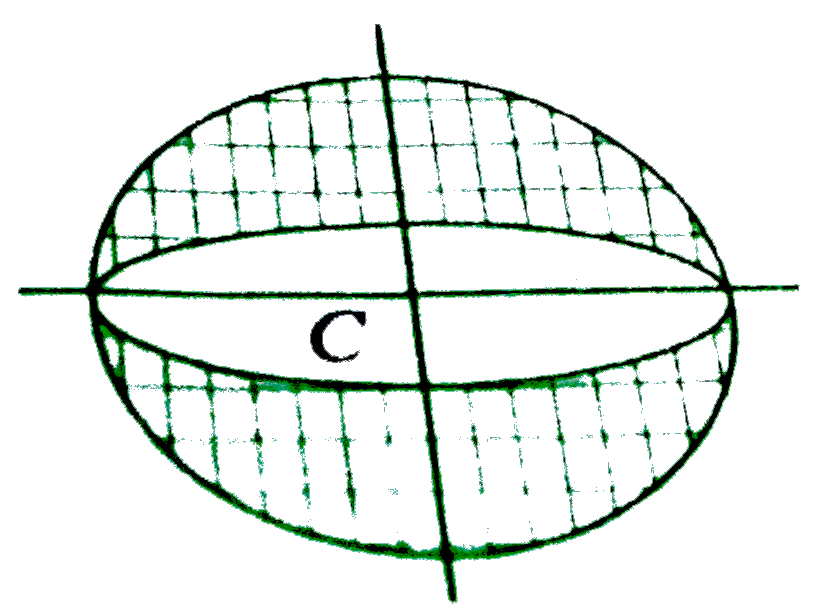
Step 2: Draw the Diagram
Draw an ellipse and inscribe a circle inside it. Label the semi-major axis of the ellipse as \( a \) and the semi-minor axis as \( b \).

Step 3: Area of the Circle and Ellipse
The area of the ellipse is given by:
\( \text{Area of ellipse} = \pi a b \)
The radius of the inscribed circle is equal to the semi-minor axis \( b \) (since the circle of maximum area inscribed in the ellipse will touch the ellipse at the points where the minor axis is). Therefore, the area of the circle is:
\( \text{Area of circle} = \pi b^2 \)

Step 4: Calculate the Probability \( p \)
The probability \( p \) that a point chosen randomly within the ellipse lies outside the circle is given by the area outside the circle divided by the area of the ellipse.

The area outside the circle is:
\( \text{Area outside circle} = \text{Area of ellipse} - \text{Area of circle} = \pi a b - \pi b^2 = \pi b(a - b) \)

Thus, the probability \( p \) can be written as:
\( p = \frac{\text{Area outside circle}}{\text{Area of ellipse}} = \frac{\pi b(a - b)}{\pi a b} = \frac{a - b}{a} \)

Step 5: Rearranging the Probability
From the expression for \( p \):
\( p = 1 - \frac{b}{a} \)
This implies:
\( \frac{b}{a} = 1 - p \)

Step 6: Finding the Eccentricity
The eccentricity \( e \) of the ellipse is given by:
\( e = \sqrt{1 - \left(\frac{b}{a}\right)^2} \)
Substituting \( \frac{b}{a} = 1 - p \):
\( e = \sqrt{1 - (1 - p)^2} \)

Step 7: Simplifying the Expression
Expanding \( (1 - p)^2 \):
\( (1 - p)^2 = 1 - 2p + p^2 \)
Thus,
\( e = \sqrt{1 - (1 - 2p + p^2)} = \sqrt{2p - p^2} \)

Final Result
The eccentricity of the ellipse is:
\( e = \sqrt{p(2 - p)} \)

Summary
The eccentricity of the ellipse is given by the expression \( e = \sqrt{p(2 - p)} \).