Two particles 1 and 2 are allowed to descend on the two fricitionless chord OA and OB of a vertical circle,at the same instant from point O.The ratio of the velocities of the particles 1 and 2 respectively,when they reach on the circumference will be (OB is the dianeter)
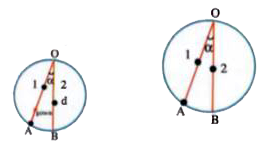
OA=d cos α,aOA=g cos α
Along OA⇒V2A=2g cos α.d cos α
Along OB
V2b=2gdimpliesVAVB=cos α
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)22videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-2)26videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE58videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER7videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III45videos
MOVING CHARGES AND MAGNETISM
Similar Questions
Two particles 1 and 2 are allowed to descend on the two frictionless chord OA and OB of a vertical circle, at the same instant from point O. The ratio of the velocities of the particles 1 and 2 respectively, when they reach on the circumference will be (OB is the diameter).
View SolutionTwo particles 1 and 2 are allowed to descend on the two frictionless chord OA and OB of a vertical circle, at the same instant from point O. The ratio of the velocities of the particles 1 and 2 respectively, when they reach on the circumference will be (OB is the diameter).
View Solution
Knowledge Check
- Question 1 - Select One
Column AIn the figure, two circle with centers A and B touch a larger circle with center O internally. The ratio of the radii of Circle A to Circle B is 7 : 9Column BOAOB
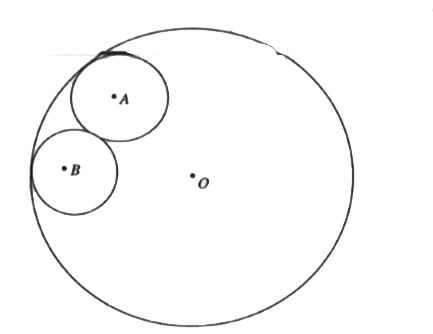 AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
A particle of mass M at rest decays into two particles of masses m1andm2 having velocities V1andV2 respectively. Find the ratio of de- Broglie wavelengths of the two particles
View SolutionIf OAandOB are two perpendicular chords of the circle r=acosθ+bsinθ epassing through origin, then the locus of the mid point of AB is :
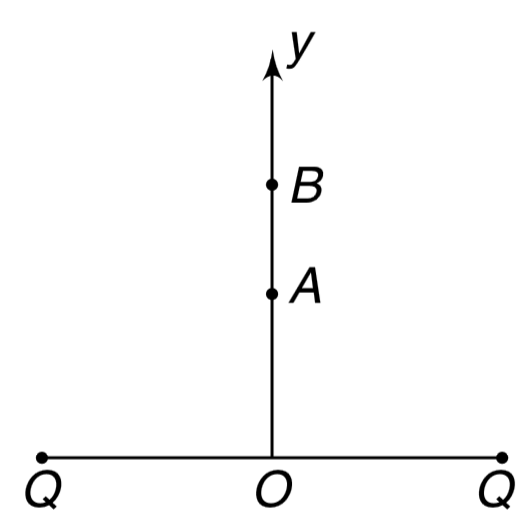
View SolutionTwo charges, Q each, are fixed on a horizontal surface at separation 2a. Line OY is vertical and is perpendicular bisector of the line joining the two charges. Another particle of mass m and charge q has two equilibrium positions on the line OY, at A and B. The distances OA and OB are in the ratio 1:3√3 (a) Find the distance of the point on the line OY where the particle will be in stable equilibrium. (b) Where will the particle experience maximum electric force – at a point above B or at a point between A and B or somewhere between O and A? Where is the acceleration of particle maximum on y axis from O to B?
 View Solution
View SolutionTangent to the circle x2+y2=a2 at any point on it in the first quadrant makes intercepts OA and OB on x and y axes respectively, O being the centre of the circle. Find the minimum value of OA+OB .
View SolutionTwo fixed point AandB are taken on the two axes such that OA=a,OB=b, two variable points C,D are taken on the same axes respectively, find the locus of the point of intersection of ADandCB if : 1OC−1OD=1OA−1OB
View SolutionAn arc AC of a circle subtends a right angle at then the center O. the point B divides the are in the ratio 1:2, If →OA=a&→OB=b. then the vector →OC in terms of a&b, is
View SolutionTwo particles are projected vertically upwards from the surface of the earth with velocities υ1=√2gR3andυ2=√4gR3 respectively. If the maximum heights attained by the two particles are h1 and h2 respectively, then calculate the ratio h1h2.
View Solution

