Two particles 1 and 2 are allowed to descend on the two frictionless chord OA and OB of a vertical circle, at the same instant from point O. The ratio of the velocities of the particles 1 and 2 respectively, when they reach on the circumference will be (OB is the diameter).
14
12
1
12√2
The correct Answer is:B
To solve the problem, we need to analyze the motion of two particles descending along two different chords of a vertical circle. Let's denote the velocities of particles 1 and 2 as VA and VB respectively when they reach the circumference of the circle.
Step 1: Analyze Particle 2 on Chord OB
For particle 2 descending along chord OB (which is the diameter of the circle), the only force acting on it is gravity. The distance it descends is equal to the diameter of the circle, which we can denote as d.
Using the third equation of motion:
V2B−U2=2as
where:
- VB is the final velocity of particle 2,
- U=0 (initial velocity),
- a=g (acceleration due to gravity),
- s=d (distance fallen).
Substituting these values, we have:
V2B=0+2gd⟹VB=√2gd
Step 2: Analyze Particle 1 on Chord OA
For particle 1 descending along chord OA, the situation is slightly different. The particle experiences a component of gravitational force along the chord. If we denote the angle between the vertical and the chord OA as α, the effective acceleration along the chord is gcos(α).
The distance fallen by particle 1 along the chord OA is also d, but we need to consider the vertical component of this distance. The vertical distance covered by particle 1 can be expressed as dcos(α).
Using the third equation of motion again:
V2A−U2=2as
where:
- VA is the final velocity of particle 1,
- U=0 (initial velocity),
- a=gcos(α) (effective acceleration),
- s=dcos(α) (vertical distance).
Substituting these values, we have:
V2A=0+2(gcos(α))(dcos(α))⟹V2A=2gdcos2(α)
Step 3: Calculate the Ratio of Velocities
Now, we can find the ratio of the velocities VA and VB:
V2AV2B=2gdcos2(α)2gd=cos2(α)
Taking the square root to find the ratio of the velocities:
VAVB=cos(α)
Final Answer
Thus, the ratio of the velocities of the particles when they reach the circumference is:
VAVB=cos(α)
For particle 2 descending along chord OB (which is the diameter of the circle), the only force acting on it is gravity. The distance it descends is equal to the diameter of the circle, which we can denote as d.
V2B−U2=2as
where:
- VB is the final velocity of particle 2,
- U=0 (initial velocity),
- a=g (acceleration due to gravity),
- s=d (distance fallen).
V2B=0+2gd⟹VB=√2gd
For particle 1 descending along chord OA, the situation is slightly different. The particle experiences a component of gravitational force along the chord. If we denote the angle between the vertical and the chord OA as α, the effective acceleration along the chord is gcos(α).
V2A−U2=2as
where:
- VA is the final velocity of particle 1,
- U=0 (initial velocity),
- a=gcos(α) (effective acceleration),
- s=dcos(α) (vertical distance).
V2A=0+2(gcos(α))(dcos(α))⟹V2A=2gdcos2(α)
Now, we can find the ratio of the velocities VA and VB:
V2AV2B=2gdcos2(α)2gd=cos2(α)
VAVB=cos(α)
Thus, the ratio of the velocities of the particles when they reach the circumference is:
VAVB=cos(α)
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Two particles are simultaneously thrown in horizontal direction from two points on a riverbank, which are at certain height above the water surface. The initial velocities of the particles are v1=5m/sandv2=7.5m/s respectively. Both particles fall into the water at the same time. First particles enters the water at a point s = 10 m from the bank. Determine
(a) the time of flight of the two particles,
(b) the height from which they are thrown,
(c) the point where the second particle falls in water.
View SolutionThe diameters of two planets are in the ratio 4:1 and their mean densities in the ratio 1:2 The acceleration due to gravity on the particles wil be in ratio.
View SolutionTwo particles AandB are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range.
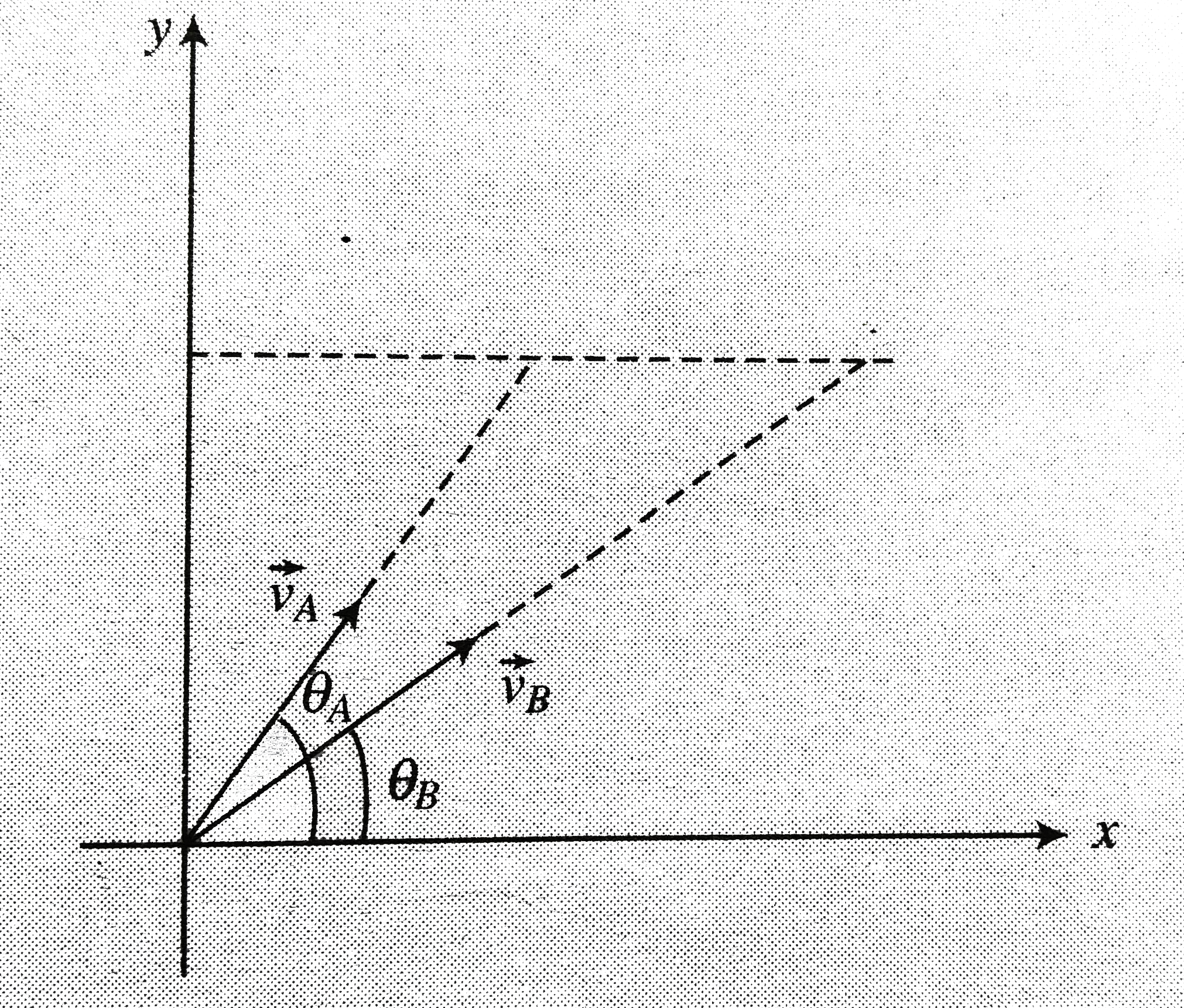 .
.
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
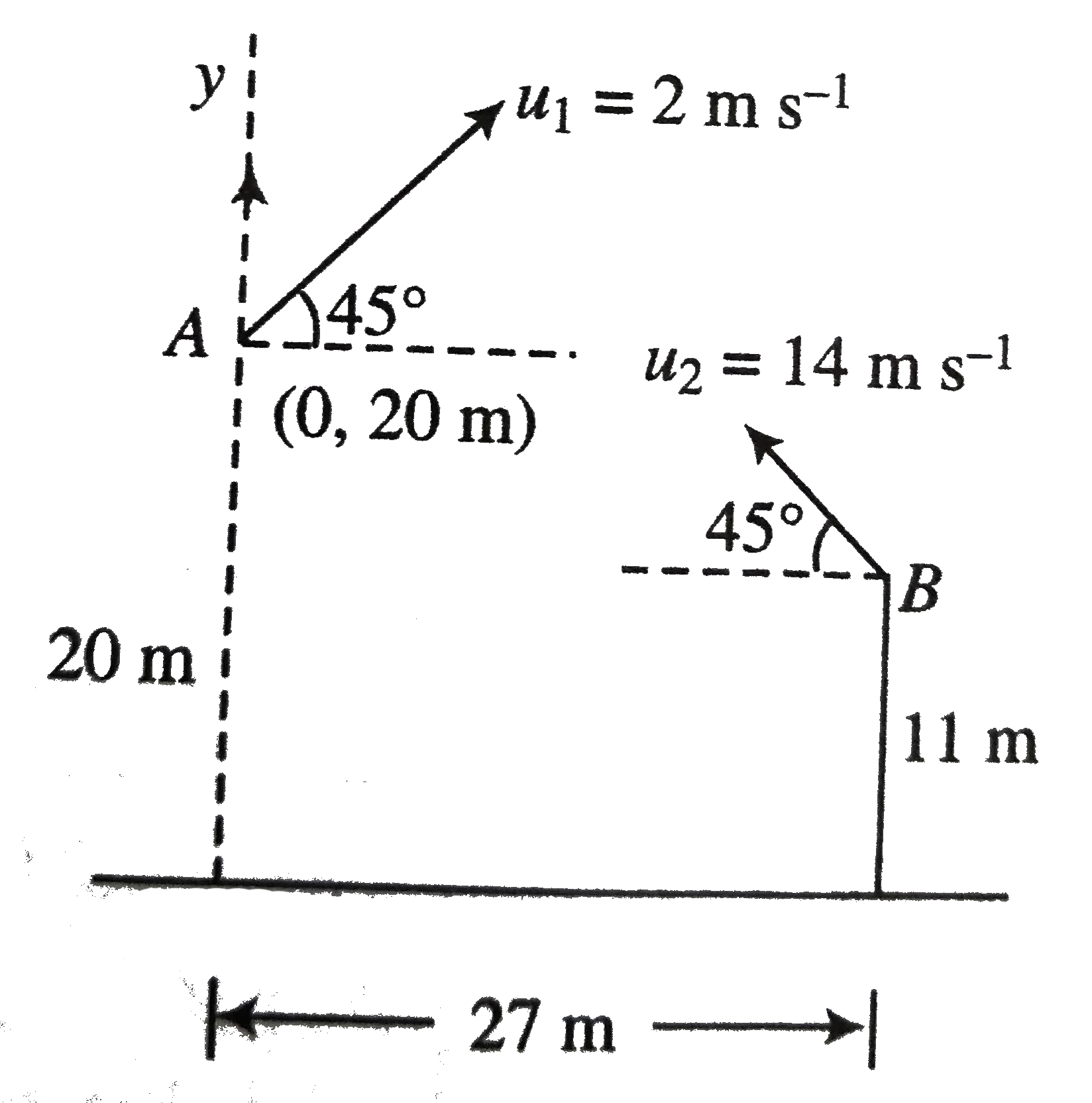
The relative velocity of B as seen from A in
View SolutionA particle is projected vertically up and another is let fall to meet at the same instant. If they have velocities equal in magnitude when they meet, the distance travelled by them are in the ratio of
View SolutionA man standing on the roof a house of height h throws one particle vertically downwards and another particle horizontally with same velocity u. Find the ratio of their velocities when they reach the earth's surface.
View SolutionTwo strings of same material are stretched to the same tension . If their radii are in the ratio 1:2 , then respective wave velocities in them will be in ratio
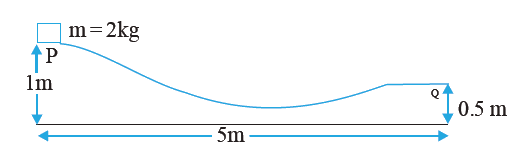
View SolutionFind the horizontal velocity of the particle when it reach the point Q. Assume the block to be frictionless. Take g=9.8m/s2.
View SolutionTwo particle move in concentric circles of radii r1 and r2 such that they maintain a straight line through the center. The ratio of their angular velocities is:
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
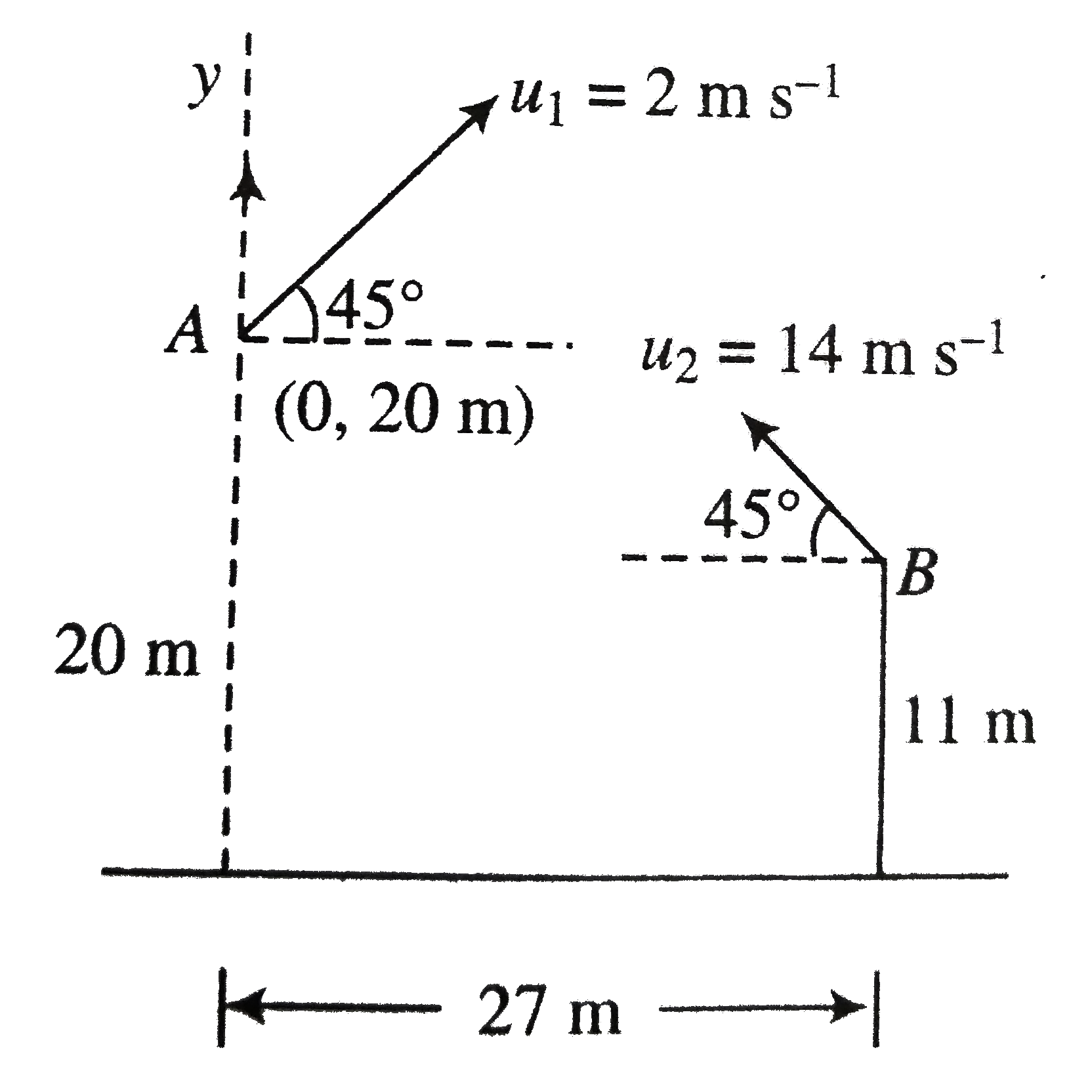
Minimum separation between A and B is
View Solution
