A jet of water with a cross sectional area 'a' is striking against a wall at an angle θ to the horizontal and rebounds elastically. If the velocity of water jet is v and the density is ρ, the normal force acting on the wall is
2av2ρcosθ
avρcosθ
2avρcosθ
avcosθ
The correct Answer is:A
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
117 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
98 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Application
6 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
6 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
16 Videos
Similar Questions
A jet of water with cross section of 6cm2 strikes a wall at an angle of 60∘ to the normal and rebounds elastically from the wall without losing energy. If the velocity of the water in the jet is 12m/s, the force acting on the wall is
View SolutionA jet water, whose cross section is A strikes a wall making an angle θ with normal and elastically rebounds. The velocity of water of density ρ is v. Force exerted on wall is :-
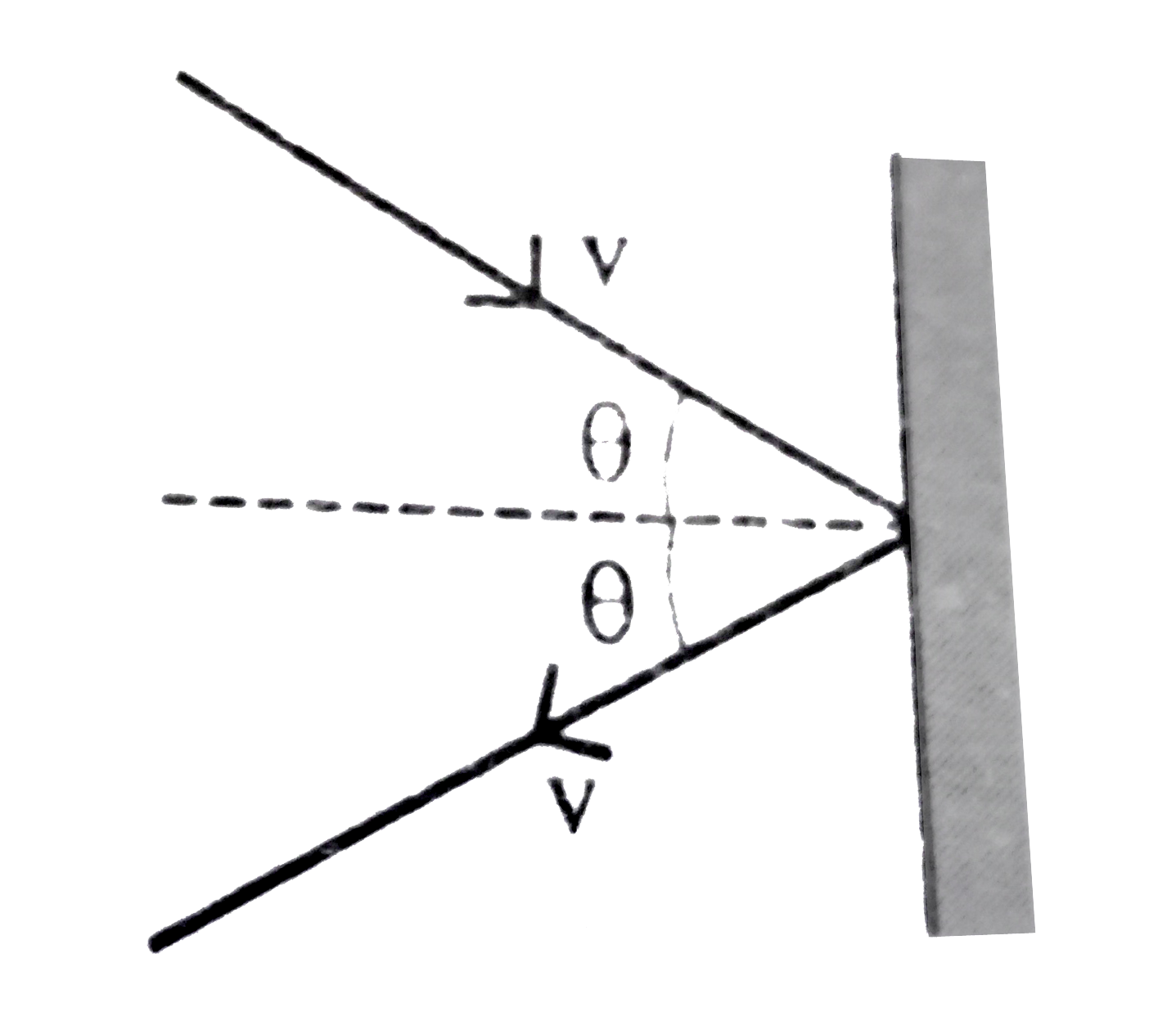
View Solution
Knowledge Check
A jet of water with cross section of 6cm2 strikes a wall at an angle of 60∘ to the normal and rebounds elastically from the wall without losing energy. If the velocity of the water in the jet is 12m/s, the force acting on the wall is
A0.864 NB86.4 NC72 ND7.2 NA jet water, whose cros section is 'a' strikes a wall making an angle θ with normal and elastically rebounds. The velocity of water of density 'd' is v. Force exerted on wall is :-
 A2av2dcosθB2av2dsinθC2avdcosθDav d cosθ
A2av2dcosθB2av2dsinθC2avdcosθDav d cosθA ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
A(θ+β)<90∘ if the wall is smoothBif the wall is rough , coefficient of restitution =tanβ/cosθCif the wall is rough, coefficient of restition
<tanβ/cotθDnone of these
A stream of particles each of mass m moving with velocity v with number of particles per unit volume n strike against a wall at an angle θ to the normal elastically. Find the pressure exerted by the exerted by the stream on the wall.
View SolutionA stream of water of density ρ, cross sectional area A, and speed u strikes a wall that is perpendicular to the direction of the stream, as shown in the figure below. The water then flows sideways across the wall. The force exerted by the stream on the wall is
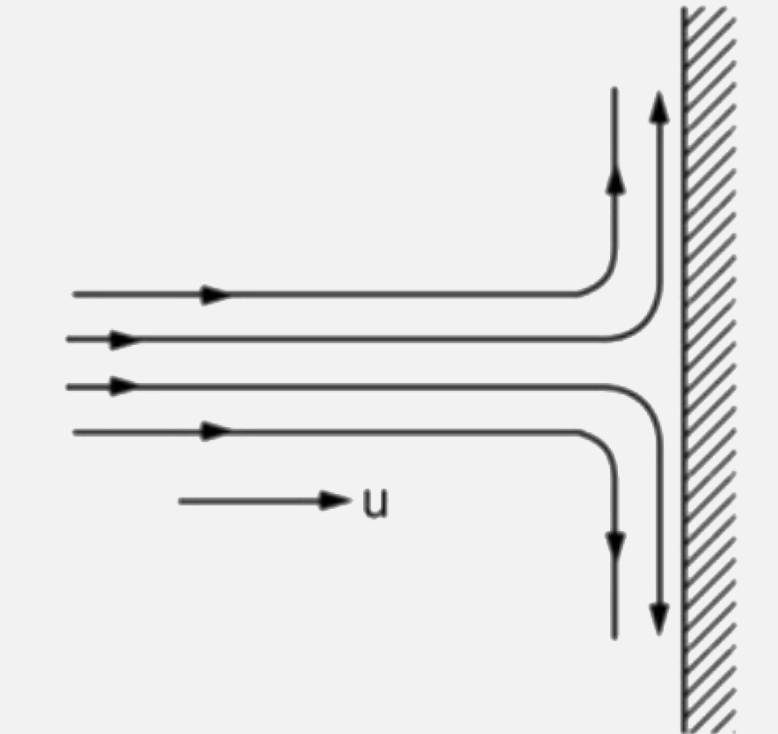
View SolutionA stream of water of density ρ, cross sectional area A, and speed u strikes a wall that is perpendicular to the direction of the stream, as shown in the figure below. The water then flows sideways across the wall. The force exerted by the stream on the wall is

View SolutionWater flows through a pipe bent at an angle α to the horizontal with velocity v . Calculate the force exerted by the water on the bend of the pipe of area of cross - section S .
View SolutionA ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
View Solution
