A block of mass m kg is pushed up against a wall by a force P that makes an angle 'θ' with the horizontal as shown in figure. The coefficient of static friction between the block and the wall is μ. The minimum value of P that allows the block to remain stationary is
Psinθ+f=mg
f=(mg−Psinθ)
μN=(mg−Psinθ)
μPcosθ=mg−Psinθ
P[sinθ+μcosθ]=mg
P=mg(sinθ+μcosθ)

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I
151 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
117 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
5 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
6 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
16 Videos
Similar Questions
A block of mass m kg is pushed up against a wall by a force P that makes an angle 'θ' with the horizontal as shown in figure . The coefficient of static friction between the block and the wall is μ . Find the minimum value of P that allows the block to remain stationary .
View SolutionA block of mass m kg is pushed up against a wall by a force P That makes an angle 'theta' with the horizontal as shown in The coefficient of static friction between the block and the wall is μ The minimum value of P that allows the block to remain stationary is .
View Solution
Knowledge Check
A block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
A2.5 NB0.98 NC4.9 ND0.49 NA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
A(a) 1.6B(b) 4.0C(c) 2.0D(d) 2.5
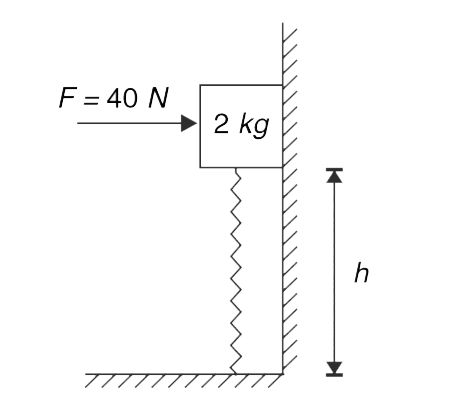
(i) In the arrangement shown in the figure the coefficient of friction between the 2 kg block and the vertical wall is μ=0.5. A constant horizontal force of 40 N keeps the block pressed against the wall. The spring has a natural length of 1.0 m and its force constant is k=400Nm–1. What should be the height h of the block above the horizontal floor for it to be in equilibrium. The spring is not tied to the block.
(ii) A block of mass M is pressed against a rough vertical wall by applying a force F making an angle of θ with horizontal (as shown in figure). Coefficient of friction between the wall and the block is μ=0.75.
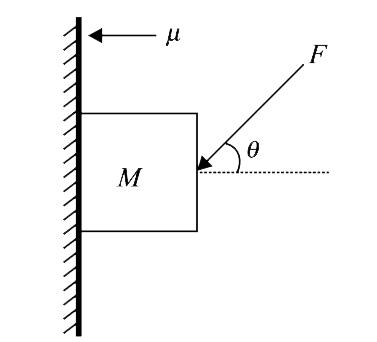
(a) If F = 2 Mg, find the range of values of θ so that the block does not slide
[Take tan37∘=0.75,sin24∘=0.4]
(b) Find the maximum value of θ above which equilibrium is not possible for any magnitude of force F.
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA block of mass m is supported on a rough wall by applying a force in figure Coefficient of static friction between block and wall is μ
For what range of value of p , the block remain in static equilibrium ?

View SolutionA block of mass m is supported on a rough wall by applying a force in figure Coefficient of static friction between block and wall is μ
For what range of value of p , the block remain in static equilibrium ?

View SolutionA block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View Solution
