Question

Figute shows the motion of a particle along a straight line.Find the average velocity of the particle during the intervals
(a)A to E, (b)B to E, (c )C to E,
(d) D to E, ( e) C to D.

Explanation

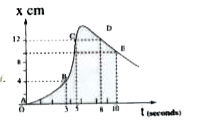
(a) As the particle moves from A to E, is the initial point and E is the final point.
The slope of the line drawn from A to E
i.e., `(Deltax)/(Deltat)` gives the average velocity during that interval of time.
The displacement `Deltax` is
`X_(E)-X_(A)`=10cm-0cm=+10cm
The time interval `Deltat_(EA)=t_(E)-t_(A)=10S`.
`therefore` During this interval average velocity
`barV=(Deltax)/(Deltat)=(+10cm)/(10S)=+1cms^(-1)`
(b)During the interval B to E. the displacement
`Deltax=x_(E)-x_(B)=10cm-4cm=6cm` and
`Deltat=t_(E)-t_(B)=10s-3s=7s.`
`Therefore` Average velocity `barV=(Deltax)/(Deltat)=(6cm)/(7s)`
=+0.857 `cms^(-1)=0.86cms^(-1)`
(c) During the interval C to E,the displacement
`Deltax=X_(E) -X_(c)=10cm0-12cm=2cm` nd
`Deltat=t_(E)-t_(c)=10s-5s=5s`
`therefore barv=(Deltax)/(Deltat)=(-2cm)/(5s)=-0.4 cms^(-1)`
(d)During the interval D to E,
the displacement
`Deltax=x_(E)-x_(D)=10cm-12cm=-2cm`
and the time interval
`Deltat=t-(E)-t_(D)`=10s-8s=2
`therefore barv=(v)=(Deltax)/(deltat)=(-2cm)/(2s)=-1cms^(-1)`
(e)During the interval C to D.the displacement
`Deltax-x_(D)-x_(c)`=12cm 12 cm=0
and the time interval
`Deltat=t_(D)-t_(c)`=8s-5s=3s
`therefore` The average velocity
`barv=(Deltax)/(Deltat)=(0m)/(3s)=0 ms^(-1)`
(The particle has reached the same position during these 3s.The average velocity is zero because the displacement is zero).