Derive the formula for the electric potential energy of system of two charges. Solution in Gujrati
Consider the charges q1 and q2 initially at infinity. Suppose, first the charge q1 is brought from infinity to the point by distance r1. There is no extermal field against which work needs to be done, so work done in bringing q1 from infinity by distancer r1 is,
∴W1=0
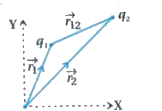
This charge q1 produces a potential in space is V1=kq1r1p
where r1p is the distance of a point P in space from the location of q1 .
Now work done in bringing charge q2 from infinity to the given point by distance r2 in the electric field of q1 is
W2=q2V1
∴W2=kq1q2r12
where r12 is the distance between points 1 and 2 at distance r1 and r2 .
Since electrostatic force is conservative this work gets stored in the form of potential energy of the system.
Potential energy of system of two charges q1 and q2 is,
U=W1+W2
∴U=kq1q2r12
If q2 was brought first to its present location and q1 brought later the potential energy would be according to equation (2).
Generally, the potential energy expression is unaltered whatever way the charges are brought to the specified locations because the path independence of work for electrostatic force.
∴U=k[0+q1q2r12+q1q3r13+q2q3r23]
∴U=k[q1q2r12+q1q3r13+q2q3r23]
Equation (2) is true for any sign of q1, and q2.
If q1q2>0 potential energy will be negative.
And if q1q2<0 potential energy will be negative .
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ( Section -A) Try Yourself50videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B Numericals16videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C5videos
ELECTROMAGNETIC WAVES
- BOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET7videos
MAGNETISM AND MATTER
Similar Questions
What are conservative force , non - conservative force , conservative field and non - conservative field ?
02:58View SolutionCalculate the potential at a point P due to a charge of 4×10−7 C located 9 cm away.
03:59View SolutionDetermine the current in each branch of the given network.
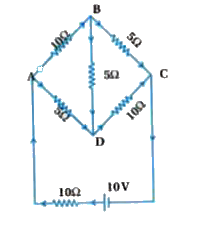 03:53View Solution
03:53View SolutionAt a place on earth the vertical component of earth's magnetic field is √3 times its horizontal component. The angle of dip at this place is …...
08:20View SolutionExplain the conept of electric potential energy.
Derive an expression for potential energy of a system of two point charges. Generalise the expression fo N discrete charges.03:05View SolutionDerive an expression for the electrostatic potential energy of a system of two point charges and find its relation with electric potential of a charge.
04:35View SolutionDerive an expression for the electric potential energy of a system of two point charges in the absence of an external electric field.
04:37View SolutionDerive an expression for electric potential energy of a system of charges in an electric field.
04:08View SolutionDerive an expression for potential energy of a system of two charges in the absence of the external electric field.
05:03View SolutionDerive the formula for the electric potential energy of system of three charges.
05:06View SolutionObtain the equation of electric potential energy of a dipole from equation of potential energy of a system of two electric charges.
03:02View SolutionDerive an expression for potential energy of a system of two point charges.
03:40View SolutionDerive an expression for potential energy of a system of two charges in an external electric field.
03:03View SolutionDerive an expression for potential energy of a system of two charges in the absence of the external electrical field.
42:27View Solutionબાહ્ય વિદ્યુતક્ષેત્રમાં બે વિદ્યુતભારોના તંત્રની સ્થિતિઊર્જા સમજાવો.
05:32View Solution

