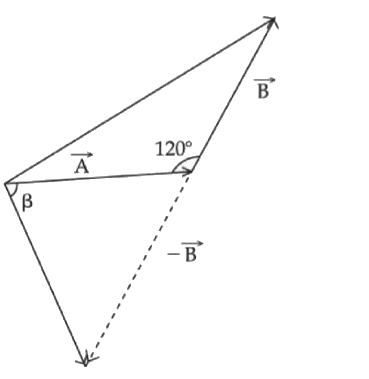
The resultant of two vectors $\to A$ and $\to b$ is perpendicular to the vector $\to A$ and its magnitude is equal to half the magnitude of vector $\to B$ . The angle between $\to A$ and $\to B$ is

$30^{\circ}$

$45^{\circ}$

$150^{\circ}$

$120^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video, text & image solution for The resultant of two vectors vecA and vecb is perpendicular to the vector vecA and its magnitude is equal to half the magnitude of vector vecB. The angle between vecA and vecB is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS MOTION IN A STRAIGHT LINE

Topper's Solved these Questions

Knowledge Check

The resultant of two vectors $\to A$ and $\to B$ is perpendicular to the vector $\to A$ and its magnitude is equal to half of the magnitude of the vector $\to B$ . Find out the angles between $\to A$ and $\to B$ .
.
A $120$
B $90$
C $60$
D $150$
The resultant of the vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between $\to A and \to B$ is :-
A $120^{\circ}$
B $150^{\circ}$
C $135^{\circ}$
DNone of these
Two vectors $\to A and \to B$ have equal magnitudes. If magnitude of $\to A + \to B$ is equal to n times the magnitude of $\to A - \to B$ , then the angle between $\to A and \to B$ is :-
A ${cos}^{- 1} (\frac{n - 1}{n + 1})$
B ${cos}^{- 1} (\frac{n^{2} - 1}{n^{2} + 1})$
C ${sin}^{- 1} (\frac{n - 1}{n + 1})$
D ${sin}^{- 1} (\frac{n^{2} - 1}{n^{3} + 1})$

MTG GUIDE-KINEMATICS -Topicwise Practice Questions (VECTORS)

Home
Ask Doubt
Profile

The resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B. .

The resultant of the vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between →A and →B is :-

Two vectors →A and →B have equal magnitudes. If magnitude of →A+→B is equal to n times the magnitude of →A−→B, then the angle between →A and →B is :-

MTG GUIDE-KINEMATICS -Topicwise Practice Questions (VECTORS)

The resultant of two vectors $\to A$ and $\to b$ is perpendicular to the vector $\to A$ and its magnitude is equal to half the magnitude of vector $\to B$ . The angle between $\to A$ and $\to B$ is

The resultant of two vectors $\to A$ and $\to B$ is perpendicular to the vector $\to A$ and its magnitude is equal to half of the magnitude of the vector $\to B$ . Find out the angles between $\to A$ and $\to B$ .
.

The resultant of the vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between $\to A and \to B$ is :-

Two vectors $\to A and \to B$ have equal magnitudes. If magnitude of $\to A + \to B$ is equal to n times the magnitude of $\to A - \to B$ , then the angle between $\to A and \to B$ is :-