Suppose that two objects A and B are moving with velocities →vA and →vB (each with respect to some common frame of refrence). Let →vAB represent the velocity of with respect to B. Then
→vAB+→vBA=0
→vAB−→vBA=0
→vAB=→vA+→–––B
|→vAB|≠|→vBA|
The correct Answer is:A
Step by step video, text & image solution for Suppose that two objects A and B are moving with velocities vecv_(A) and vecv_(B) (each with respect to some common frame of refrence). Let vecv_(AB) represent the velocity of with respect to B. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs31videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (UNIFORM CIRCULAR MOTION)8videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS32videos
GRAVITATION
- BOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)24videos
LAWS OF MOTION
Similar Questions
STATEMENT -1 : For an observer looking out through the window of a fast moving train , the nearby objects appear to move in the opposite direction to the train , while the distant objects appear to be stationary .
STATEMENT - 2 : If the observer and the object are moving at velocities →v1 and →v2 respecttively with refrence to a laboratory frame , the velocity of the object with respect to a laboratory frame , the velocity of the object with respect to the observer is →v2−→v(1) .
(a) Statement -1 is True, statement -2 is true , statement -2 is a correct explanation for statement -1
(b) Statement 1 is True , Statement -2 is True , statement -2 is NOT a correct explanation for statement -1
(c) Statement - 1 is True , Statement -2 is False
(d) Statement -1 is False, Statement -2 is TrueView SolutionA particle moves along the x' axis of frame S' with velocity 0.50c. Frame S' moves with velocity 0.80c with respect to frame S. What is the velocity of the particle with respect to frame S?
View Solution
Knowledge Check
- Question 1 - Select One
Two objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
AvA−vBBvA+vBCvB−vADvA/vB - Question 2 - Select One
Two objects A and B are moving with velocities vAandvB respectively along positive x-axis. If vA<vB then, which of the following position-time graphs is correctly showing the velocity of A and B ?
A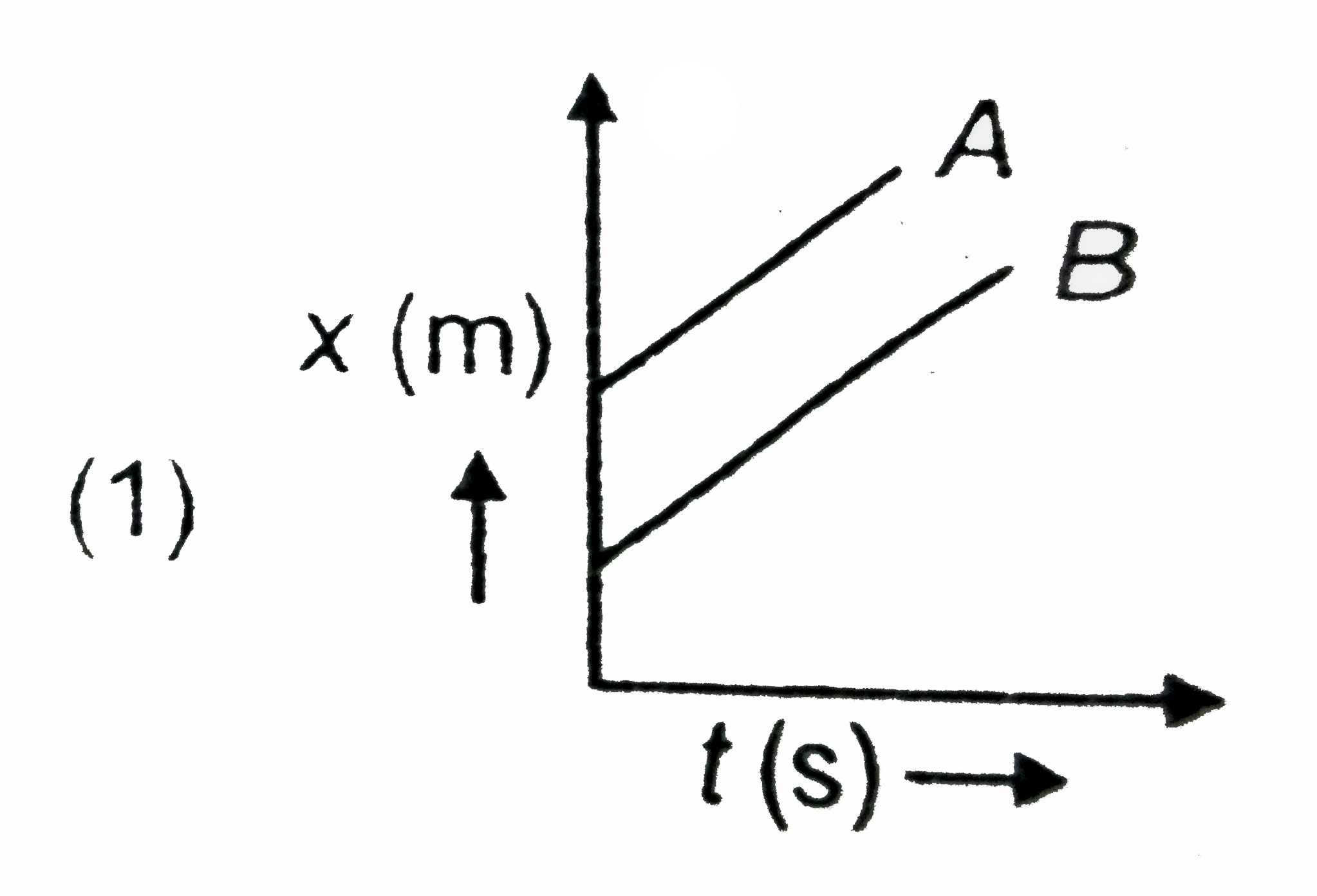 B
B C
C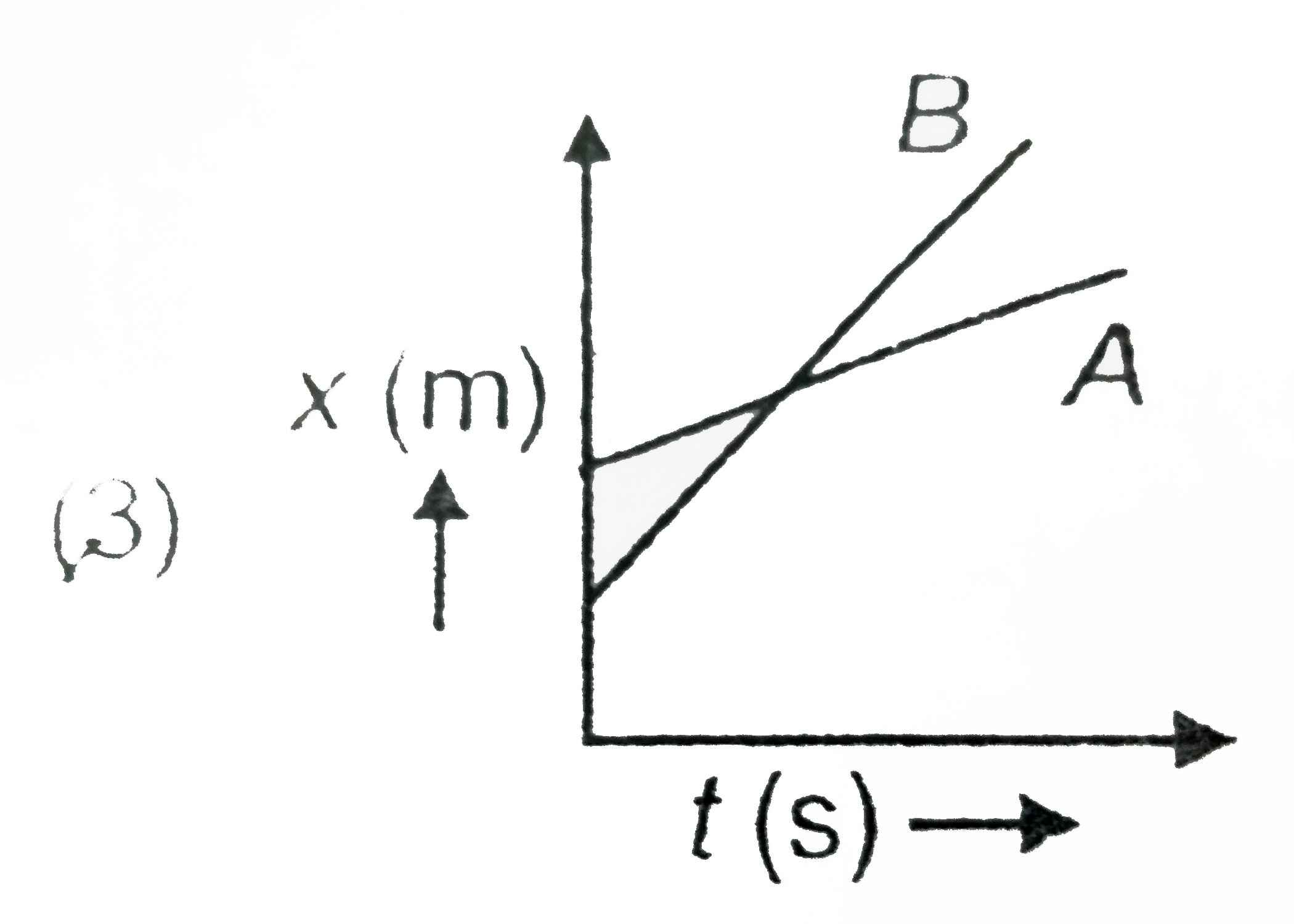 D
D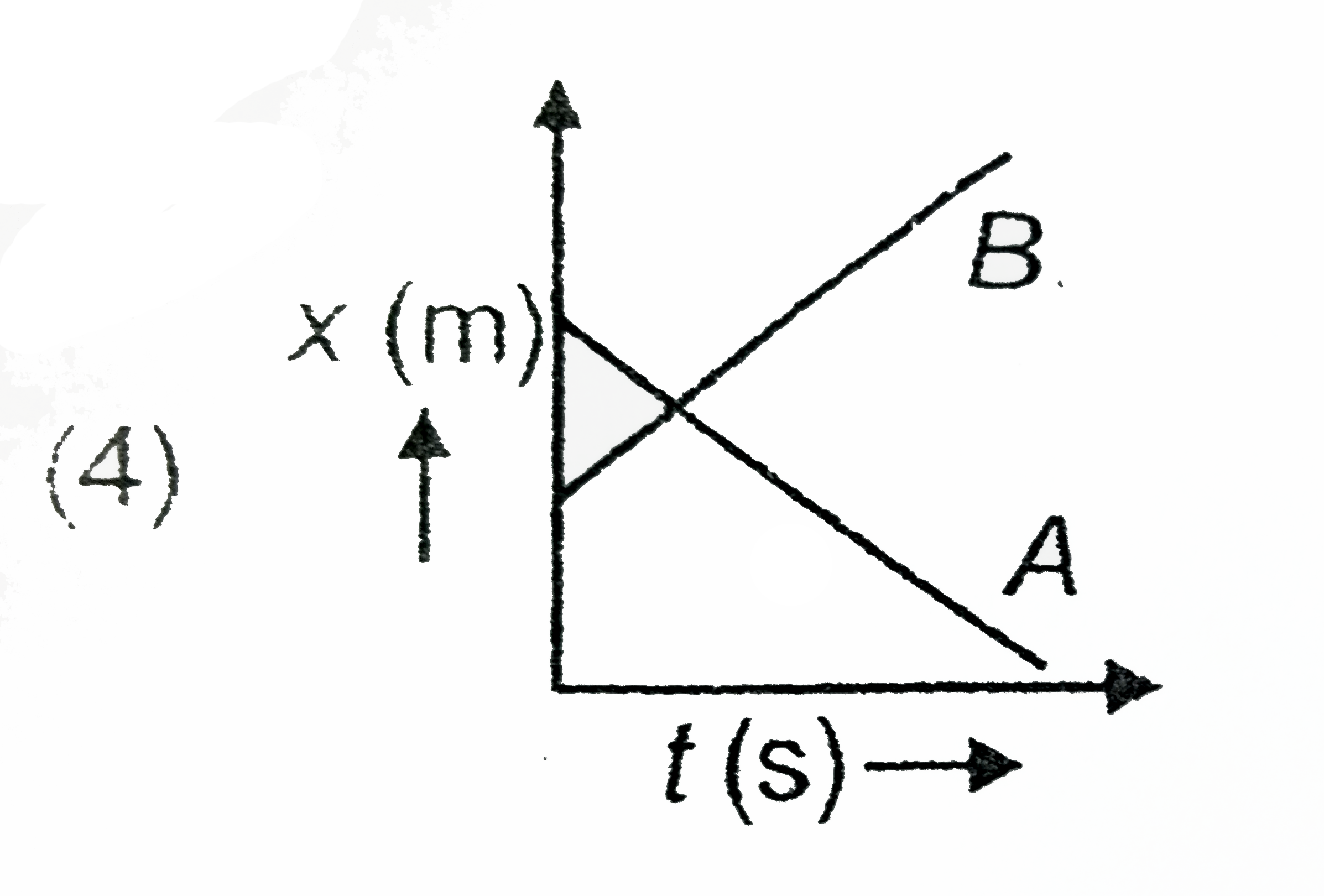
- Question 3 - Select One
Two rough blocks A and B ,A placed over B move with acceleration →aA and →aB veclocities →v(A) and →vB by the action of horizontal forces −→FA and −→FB, respectively. When no friction exsits between the blocks A and B,
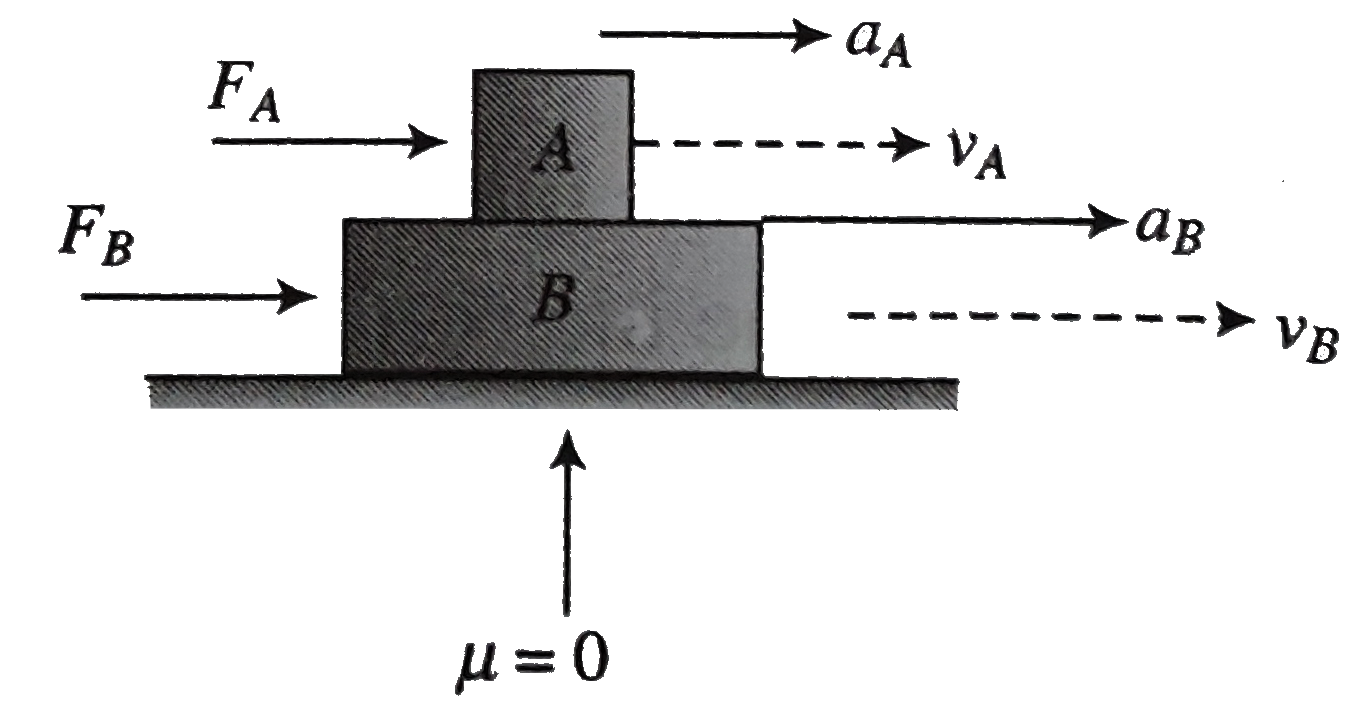 AvA=vBBaA=aBCBoth (a) and (b)DNone of the Above
AvA=vBBaA=aBCBoth (a) and (b)DNone of the Above
Assertion : An object has given two velocities →v1 and →v2 has a resultant velocity →v=→v1+→v2.
Reason : →v1and→v2 should be velocities with reference to some common reference frame.View SolutionForce on a charged particle moving with velocity →v subjected to a magnetic field is zero. This means:
View SolutionTwo frames of reference P and Q are moving relative to each other at constant velocity. Let →vOP and →aOP represent the velocity and the acceleration respectively of a moving particle O as measured by an observer in frame P and →VOQ and →aOQ represent the velocity and the acceleration respectively of the moving particle O as measured by an observer in frame Q, then
View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is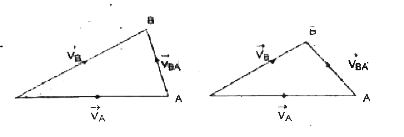 View Solution
View SolutionThe velociies of A and B are →vA=2ˆi+4ˆjand→vB=3ˆi−7ˆj , velocity of B as observed by A is
View Solution

