If polars of A,B w.r.t to the circle having centre O and radius r intersect at P then OA2−OB2=AP2−BP2
The correct Answer is:=Ap2−Bp2
Topper's Solved these Questions
- CIRCLESBOOK - AAKASH SERIESCHAPTER - CIRCLESEXERCISE - EXERCISE 1.1 (VERY SHORT ANSWER QUESTIONS)
6 Videos
- CIRCLESBOOK - AAKASH SERIESCHAPTER - CIRCLESEXERCISE - EXERCISE 1.1 ( SHORT ANSWER QUESTIONS)
3 Videos
- CIRCLESBOOK - AAKASH SERIESCHAPTER - CIRCLESEXERCISE - PRACTICE EXERCISE
164 Videos
- CIRCLEBOOK - AAKASH SERIESCHAPTER - CIRCLEEXERCISE - EXERCISE -1.4
38 Videos
- COMPLEX NUMBERSBOOK - AAKASH SERIESCHAPTER - COMPLEX NUMBERSEXERCISE - PRACTICE EXERCISE
93 Videos
Similar Questions
Knowledge Check
A and B are two points on the hyperbola O is the centre. If OA is perpendicular to OB then 1(OA)2+1(OB)2 is equal to
A1a2+1b2B1a2−1b2C1b2−1a2Da2+b2Polar of origin (0, 0) w.r.t. the circle x2+y2+2λx+2μy+c=0 touches the circle x2+y2=r2 if
Ac=r(λ2+μ2)Br=c(λ2+μ2)Cc2=r2(λ2+μ2)Dr2=c2(λ2+μ2)Tangent at A(3,4) of circle x2+y2=25 meet x and y axis at P and Q if a circle having centre as incentre of ΔOPQ and passing through origin has radius r then r2 is
A62572B625256C62564D62532
If A and B are conjugate points w.r.t to circle x2+y2=r2 then OA2+OB2=
View SolutionIn the figure below, CD is a chord of the semi circle with centre O.
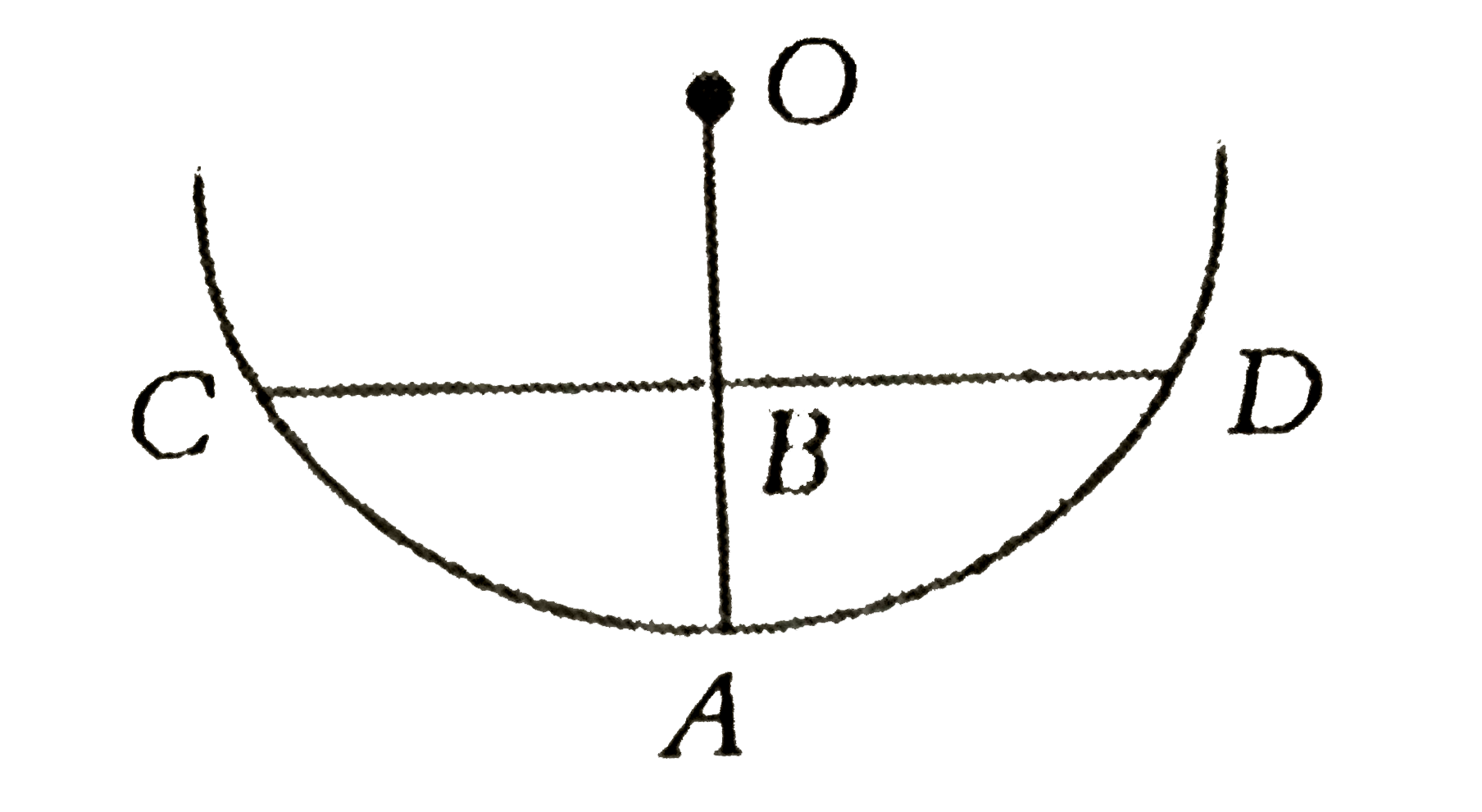 OA is the radius of the circle. If CD=10 cm, AB=2 cm and ¯¯¯¯¯¯OA⊥¯¯¯¯¯¯CD the length of OB is _____________
OA is the radius of the circle. If CD=10 cm, AB=2 cm and ¯¯¯¯¯¯OA⊥¯¯¯¯¯¯CD the length of OB is _____________
View SolutionIn the figure below, CD is a chord of the semi circle with centre O.
 OA is the radius of the circle. If CD=10 cm, AB=2 cm and ¯¯¯¯¯¯OA⊥¯¯¯¯¯¯CD the length of OB is _____________
OA is the radius of the circle. If CD=10 cm, AB=2 cm and ¯¯¯¯¯¯OA⊥¯¯¯¯¯¯CD the length of OB is _____________
View SolutionTangent at A(3,4) of circle x2+y2=25 meet x and y axis at P and Q if a circle having centre as incentre of ΔOPQ and passing through origin has radius r then r2 is
View SolutionIn the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
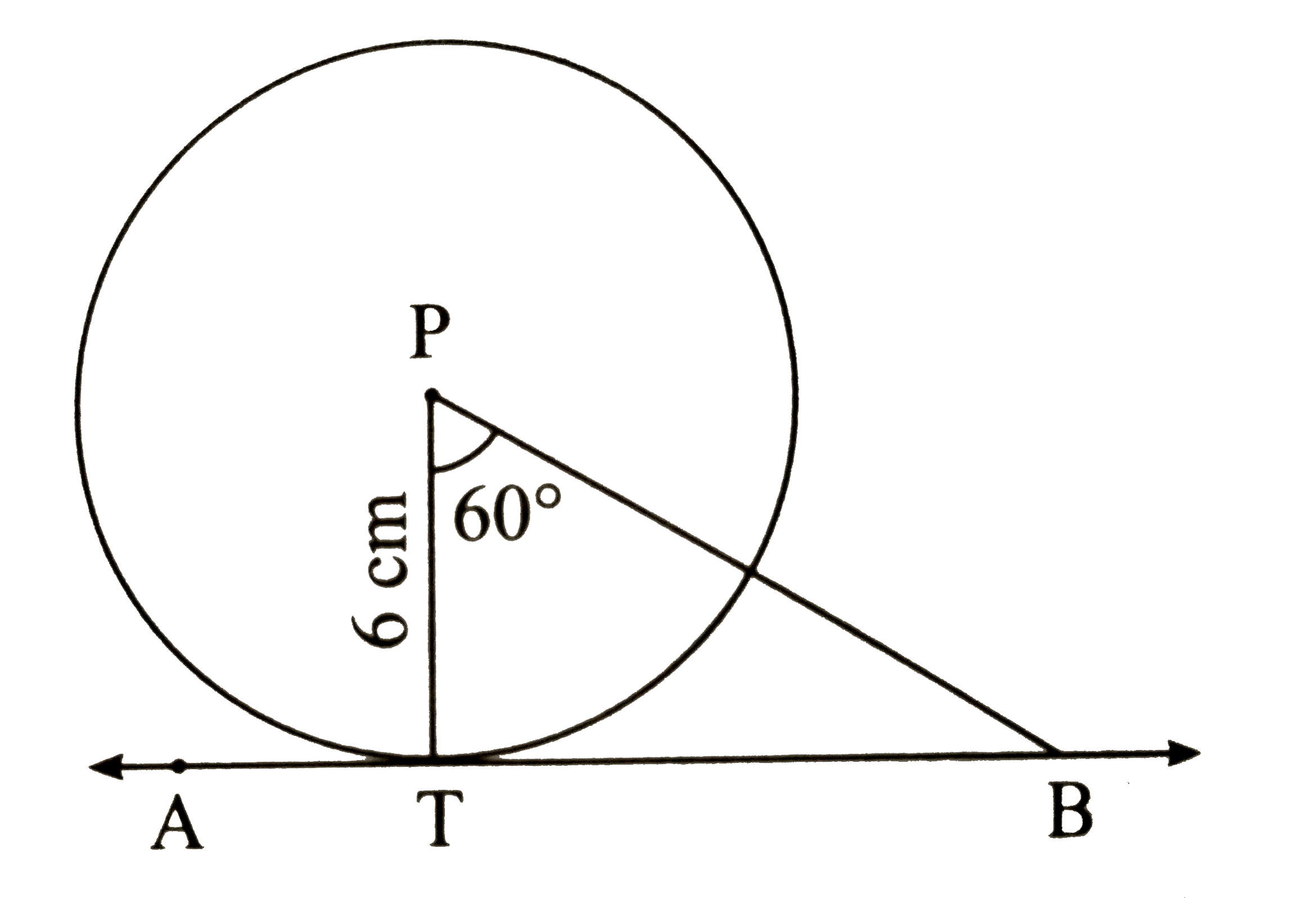
View Solution
