Each side of is the polar of the opposite vertex with respect to a circle with centre P. Then P is ortho centre of .
The correct Answer is:the circle
Topper's Solved these Questions
- CIRCLESBOOK - AAKASH SERIESCHAPTER - CIRCLESEXERCISE - EXERCISE 1.1 (VERY SHORT ANSWER QUESTIONS)
6 Videos
- CIRCLESBOOK - AAKASH SERIESCHAPTER - CIRCLESEXERCISE - EXERCISE 1.1 ( SHORT ANSWER QUESTIONS)
3 Videos
- CIRCLESBOOK - AAKASH SERIESCHAPTER - CIRCLESEXERCISE - PRACTICE EXERCISE
164 Videos
- CIRCLEBOOK - AAKASH SERIESCHAPTER - CIRCLEEXERCISE - EXERCISE -1.4
38 Videos
- COMPLEX NUMBERSBOOK - AAKASH SERIESCHAPTER - COMPLEX NUMBERSEXERCISE - PRACTICE EXERCISE
93 Videos
Similar Questions
Knowledge Check
The equations of the sides AB and CA of a ΔABC are x+2y=0 and x−y=3 respectively. Given a fixed point P(2, 3).
Q. If P be orthocentre of ΔABC then equation of side BC is :Ay+5=0By−5=0C5y+1=0D5y−1=0In the figure ΔABCis inscribed in a circle with centre O. If ∠ABC=30∘ then ∠ACBis equal to
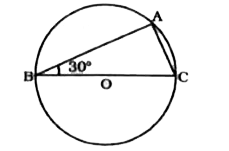 A30∘B60∘C50∘D90∘
A30∘B60∘C50∘D90∘Sides of ΔABC are in A.P. if a <min{b,c} then cosA is equal to
A4c−3b2bB4c−3b2cC3c−4b2cD4b−3c2b
A Rhombus ABCD has sides of length 10. A circle with centre ‘A’ passes through C (the opposite vertex) likewise, a circle with centre B passes through D. If the two circles are tangent to each other. Find the area of the rhombus.
View SolutionThe circumferences of three unequal circles whose centres are A, B and C pass througha common point, O, from which lines are drawn through A, B and C meeting the circumferences at A', B' and C". Show that the sides of ΔA'B'C' pass through the other points of intersection of the circles and are respectively parallel to the sides of the ΔABC
View SolutionThe equations of the sides AB and CA of a ΔABC are x+2y=0 and x−y=3 respectively. Given a fixed point P(2, 3).
Q. If P be orthocentre of ΔABC then equation of side BC is :
View SolutionFor the four circles M, N, O and P, following four equations are given :
Circle M : x2+y2=1
Circle N : x2+y2–2x=0
Circle 0 : x2+y2−2x−2y+1=0
Circle P : x2+y2–2y=0
If the centre of circle M is joined with centre of the circle N, further centre of circle N is joined with centre of the circle O, centre of circle O is joined with the centre of circle P and lastly, centre of circle P is joined with centre of circle M, then these lines form the sides of a :
View SolutionA circle touches the side BC of ΔABC at P and touches AB and AC produced at Q and R respectively. Prove that AQ=1/2(Perimeter of ΔABC).
View Solution
