If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Given : Two circles C(O,r) intersecting at points A and B.
To prove : OO' is the perpendicular bisector of AB.
Construction : Draw line segment OA,OB,O'A and O'B Let OO' and AB intersect at M.
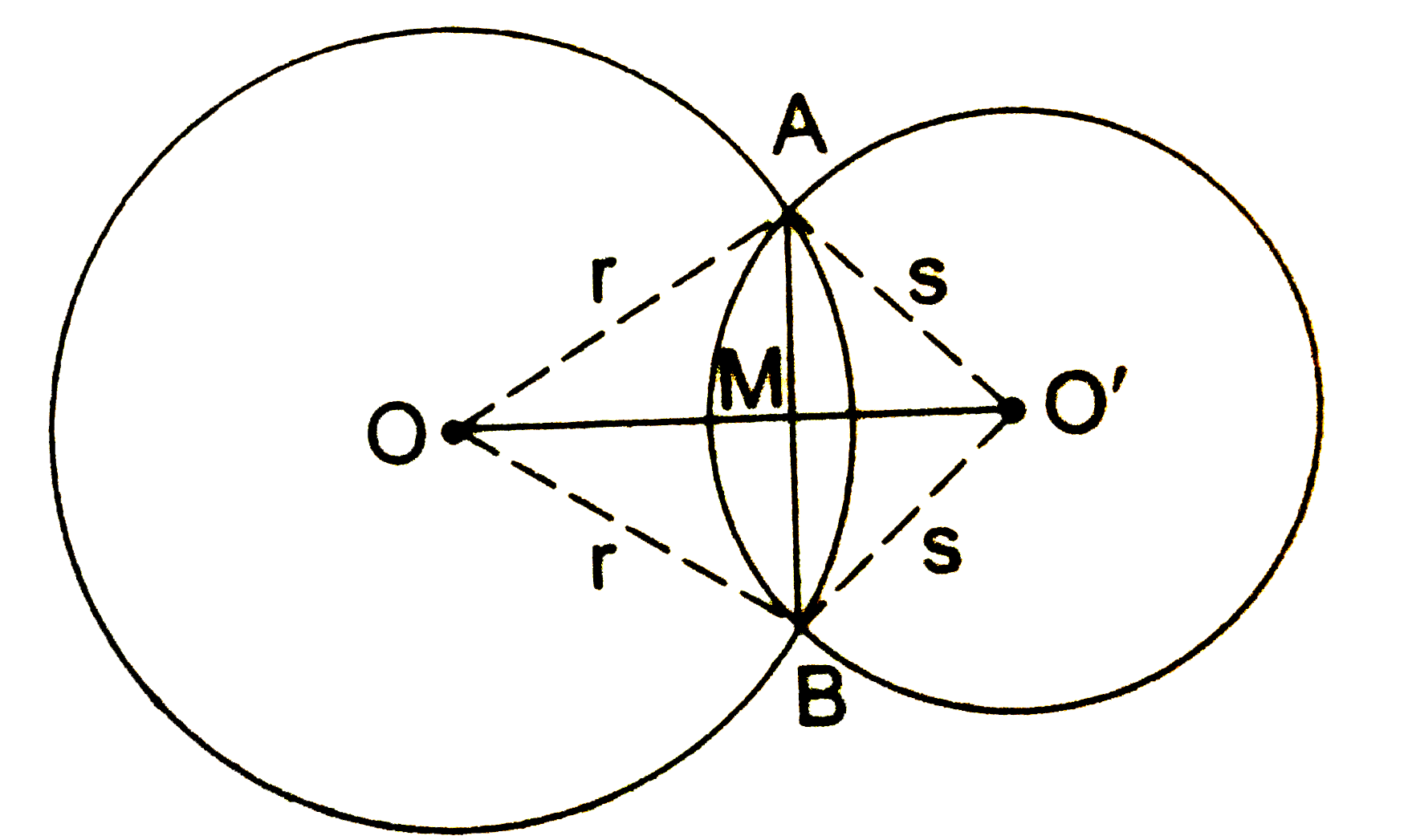
Proof : In ΔOAO' and ΔOBO' , we have
OA = OB [each equal to r]
O'A = O'B [each equal to s ]
OO'=OO' [common]
∴ΔOAO'≅ΔOBA'[by SSS-congurence]
⇒∠AOO'=∠BOO'
⇒∠AOM=∠BOM .....(i)
[∵∠AMO+∠BMO=180∘ and ∠BOO'=∠BOM].
In ΔAOM and ΔBOM , we have
OA=AB [each equal to r ]
∠AOM=∠BOM[ from (i) ]
OM=OM [ common]
⇒ΔAOM≅ΔBOM [ by SAS - congurence ]
⇒AM=BM and ∠AMO=∠BMO
⇒AM=BM and ∠AMO=∠BMO=90∘
[∵∠AMO+∠BMO=180∘ and ∠AMO=∠BMO]
⇒OO' is the perpendicualr bisector of AB.
Similar Questions
Knowledge Check
- Question 1 - Select One
If two equal circles are such that the centre of one lies on e circumference of the other, then the ratio of the common chord of two circles to the radius of any of the circles is :
A√3:2B√3:1C√5:1Dnone of the above
Theorem:- 3 There is one and only one circle passing through three non collinear points and If two circles intersects in two points; then the line joining the centres is perpendicular bisector of common chords
View SolutionTwo circles itnersect each other in two points. Prove that the line through their centres is the perpendicular bisector of the common chord.
View SolutionIf a number of circles touch line segment PQ at a point A then , their centres lie on the perpendicular bisector of PQ. State True or False
View SolutionTwo circles of radii 5 cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
Let the common chord be AB and Pand Q be the centers of the two circles.
AP=5cmand AQ=3cm.
PQ=4cm ...given
Now, segPQ⊥chordAB
AR=RB=12AB....perpendicular from center to the chord, bisects the chord
Let PR=xcm
so RQ=(4−x)cm
In△ARP,AP2=AR2+PR2
AR2=52−x2...(1)
In △ARQ,AQ2=AR2+QR2
AR2=32−(4−x)2...(2)
52−x2=32−(4−x)2...from (1) & (2)
25−x2=9−(16−8x+x2)
25−x2=−7+8x−x2
32=8x
x=4 substituting in equation(1) we get , AR2=25−16=9
AR=3cm
AB=2×AR=2×3=6
AB=6cmSo length of common chord is6 cm.View SolutionTwo circles of radil 5cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
View SolutionIf a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two distinct points. Their centres are 4 cm apart. Find the length of their common chord.
View Solution

