In the adjoining figure, OPQR is a square. A circle drawn with centre O cuts the square in X and Y. Prove that QX = QY
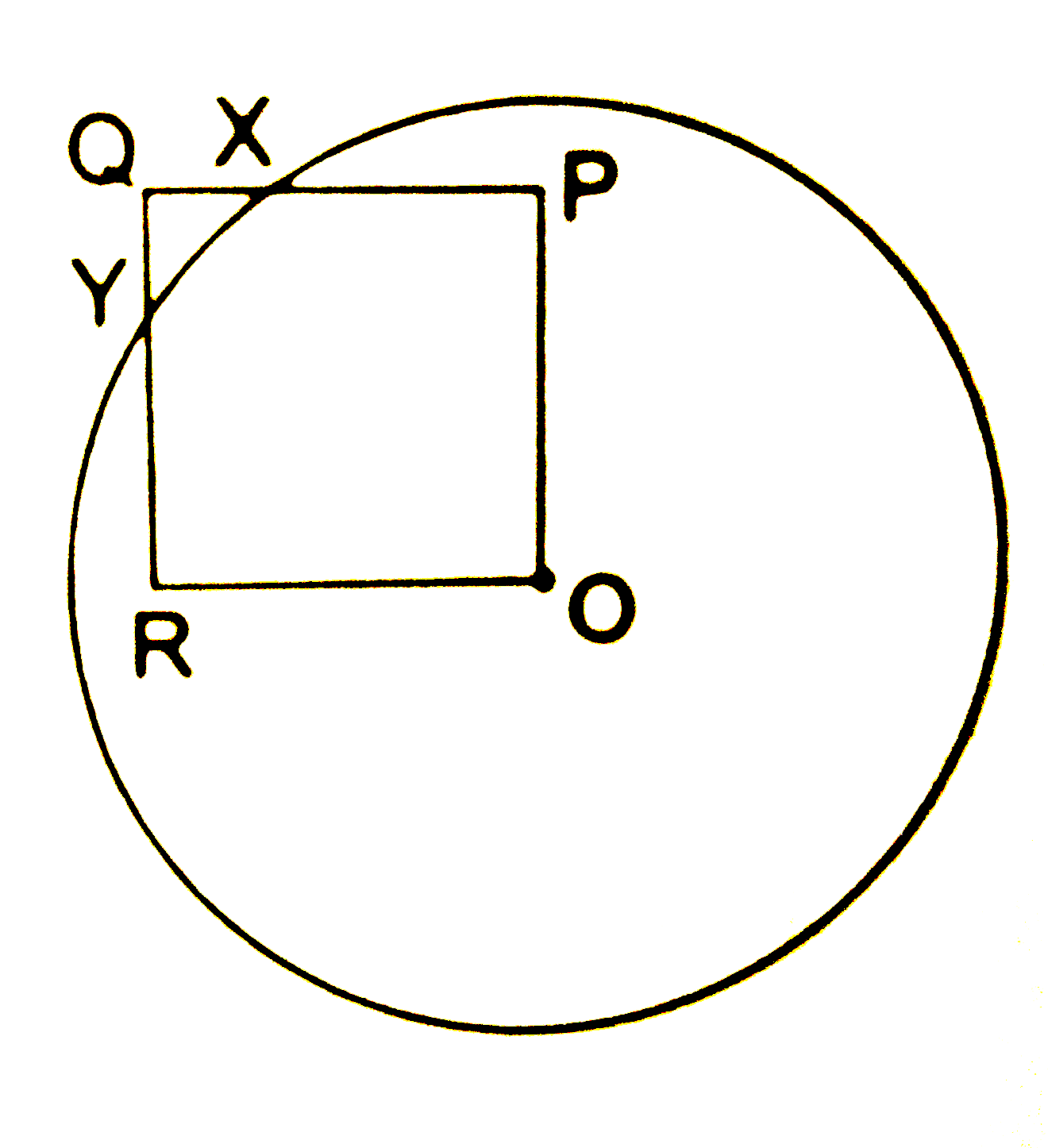
Video Solution
Text Solution
ΔOXP≅ΔOYR.[∵OP=OR,OX=OY=r and ∠OPX=∠ORY=90∘]
⇒PX=RY⇒PQ−PX=QR−RY[∵PQ=QR]
⇒QX=QY
|
Similar Questions
Knowledge Check
In the adjoining figure, O is the centre of circle. If ∠DAB=50∘ find the values of x and y.
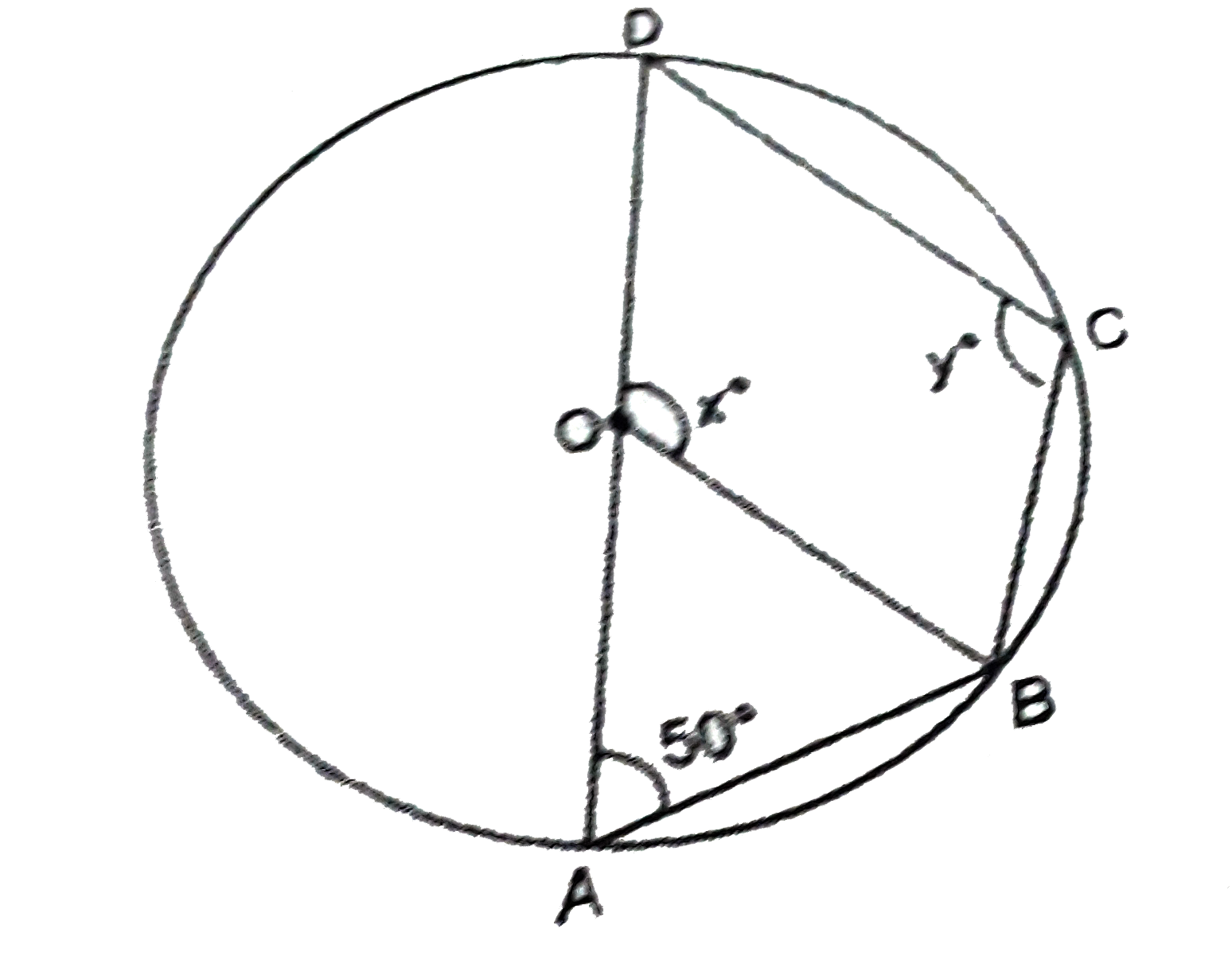 Ax=110∘,y=70∘Bx=90∘,y=90∘Cx=100∘,y=80∘Dx=130∘,y=50∘
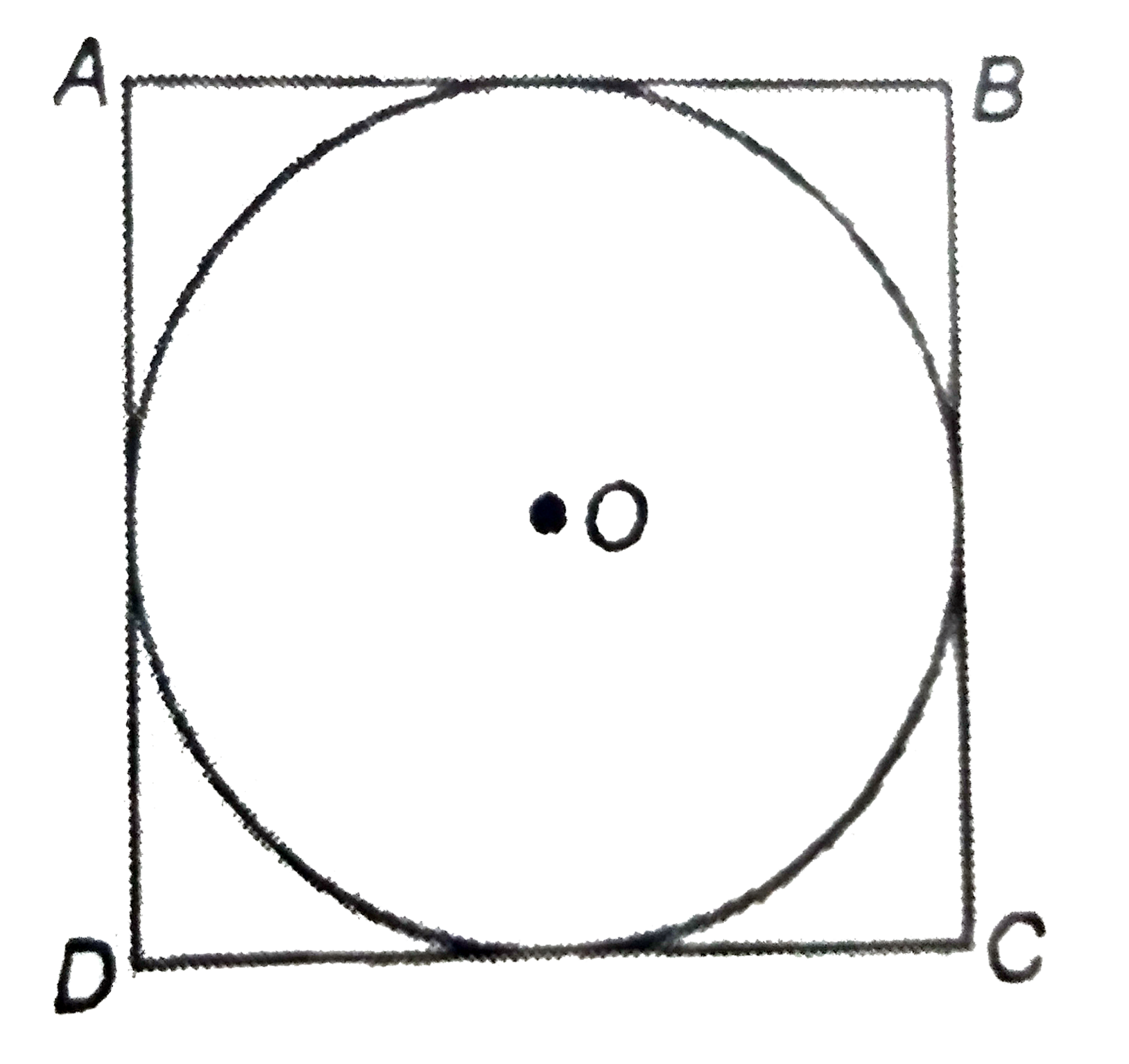
Ax=110∘,y=70∘Bx=90∘,y=90∘Cx=100∘,y=80∘Dx=130∘,y=50∘In the adjoining figure ABCD is a square . A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square , AD and BC are the respective diameters of the two smaller circles. Area of the square is 16cm2.
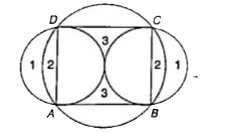
What is the area of region 2 ?A3(π−2)cm2B(π−3)cm2C(2π−3)cm2D4(π−2)cm2In the adjoining figure ABCD is a square . A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square , AD and BC are the respective diameters of the two smaller circles. Area of the square is 16cm2.
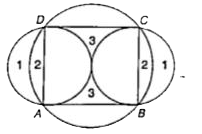
What is the area of region 3 ?A(4−4π)cm2B4(4−π)cm2C(4π−2)cm2D(3π+2)cm2
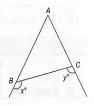
In the adjoining figure, x>y, Prove that AB>AC
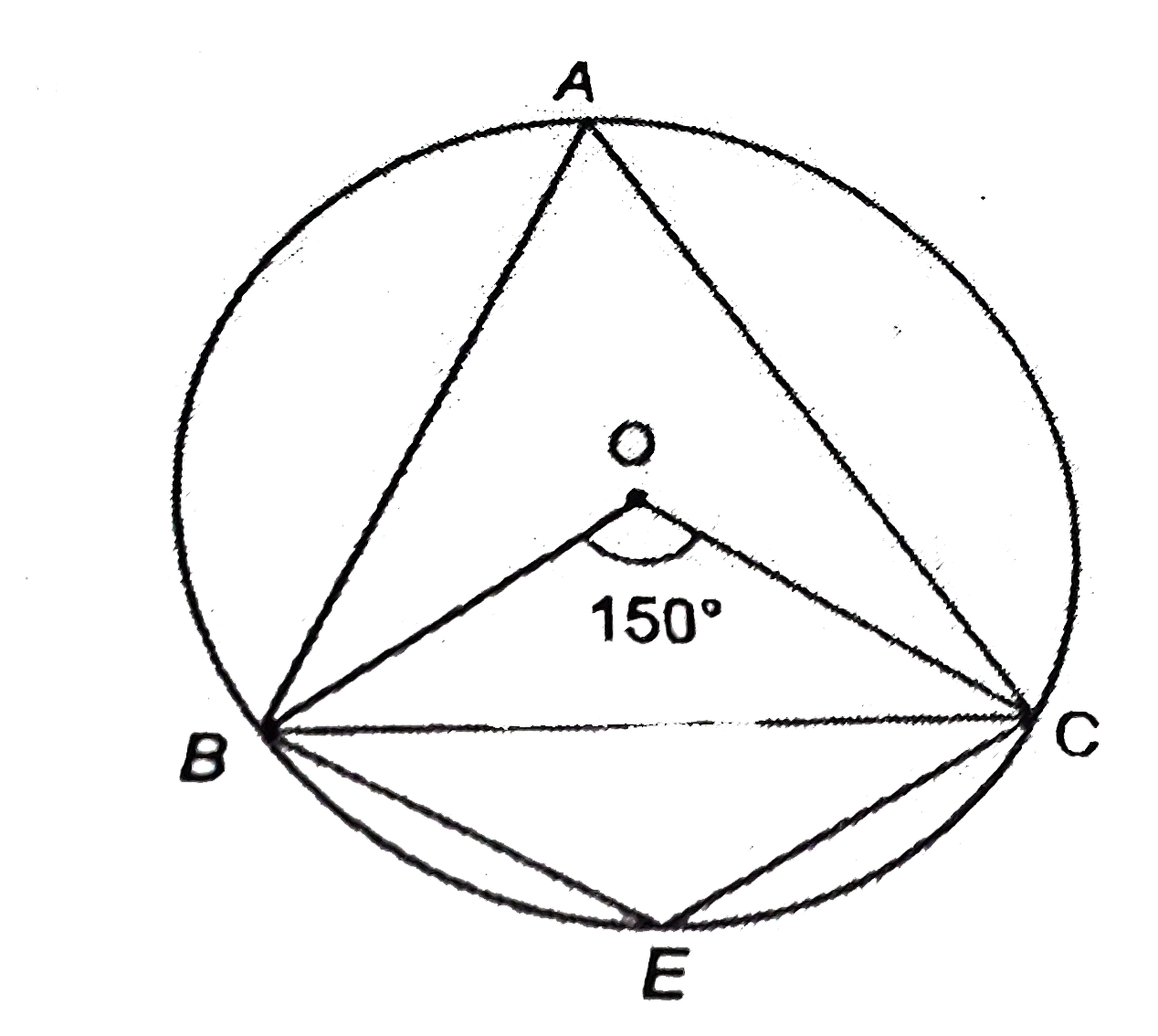
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
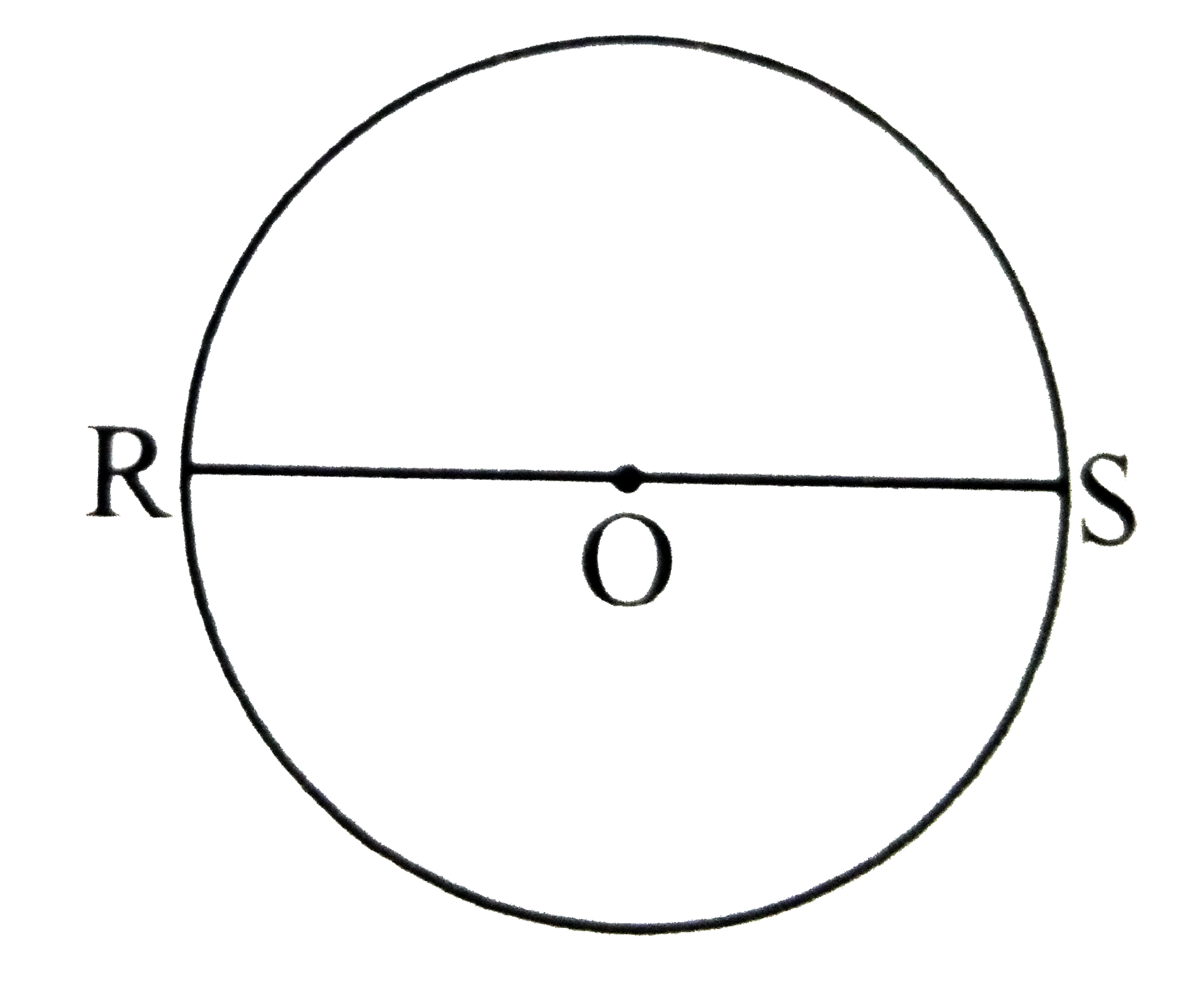
View SolutionIn the adjoining figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠RTS is an acute angle.
View SolutionIn the adjoining figure ABCD is a square . A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square , AD and BC are the respective diameters of the two smaller circles. Area of the square is 16cm2.
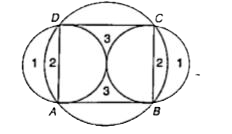
What is the area of region 1 ?
View SolutionIn the adjoining figure, O is the centre of the circle, Then x=?

View Solution