In the given figure, OPOR is a square. A circle drawn with centre O, cuts the square X and Y. Prove that QX=QY.
Step by step video & image solution for In the given figure, OPOR is a square. A circle drawn with centre O, cuts the square X and Y. Prove that QX=QY. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. The value of x is
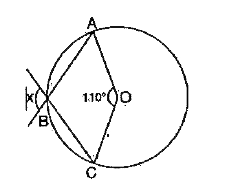 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘In the given figure, ABCD is a square. A line segment DX cuts the side BC at X and the diagonal AC at O such that <COD=105∘ and <OXC=x. The value of x is
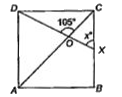 A40∘B60∘C80∘D85∘
A40∘B60∘C80∘D85∘In the given figures, value of y (O is the centre of the circle) is
 A100∘B120∘C130∘D140∘
A100∘B120∘C130∘D140∘
In the given figure, if O is centre of circle, then ∠PQR=
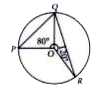
View SolutionIn a given figure, O is centre of circle then ∠x+∠y = ?

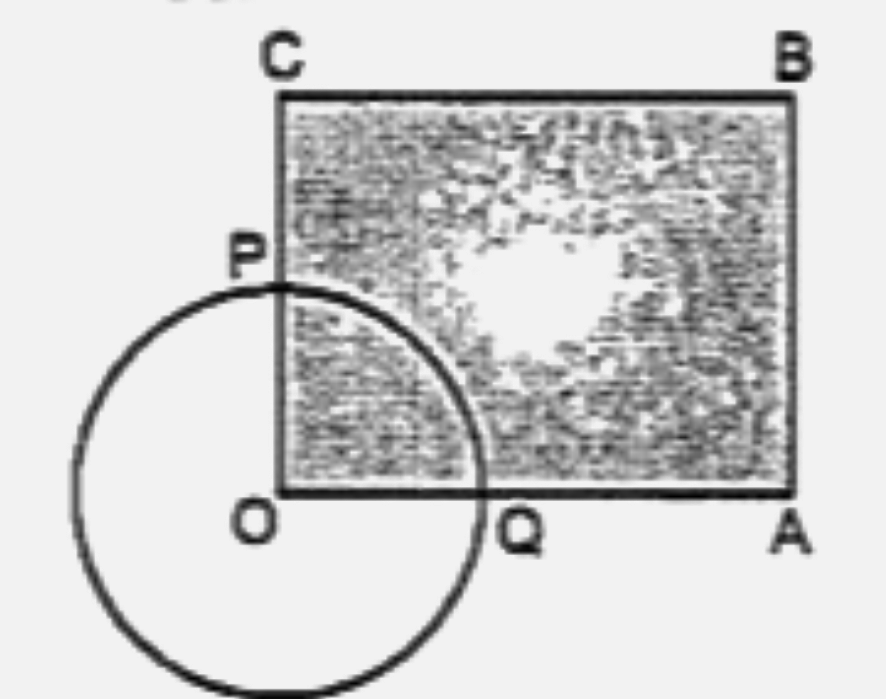
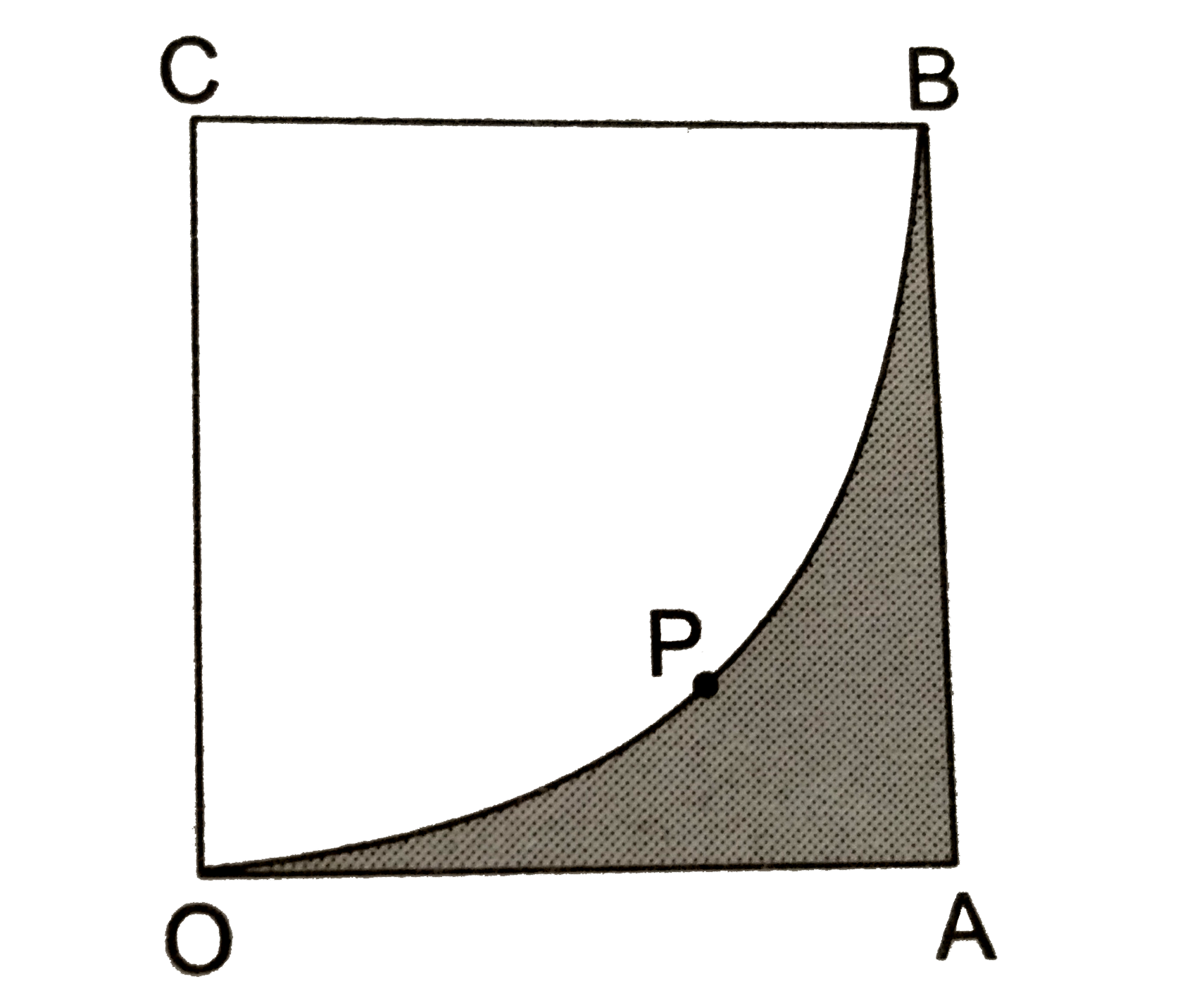
View SolutionIn the given figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region.

View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre O from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionIn the given figure, OABC is a square of side 7cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
View Solution