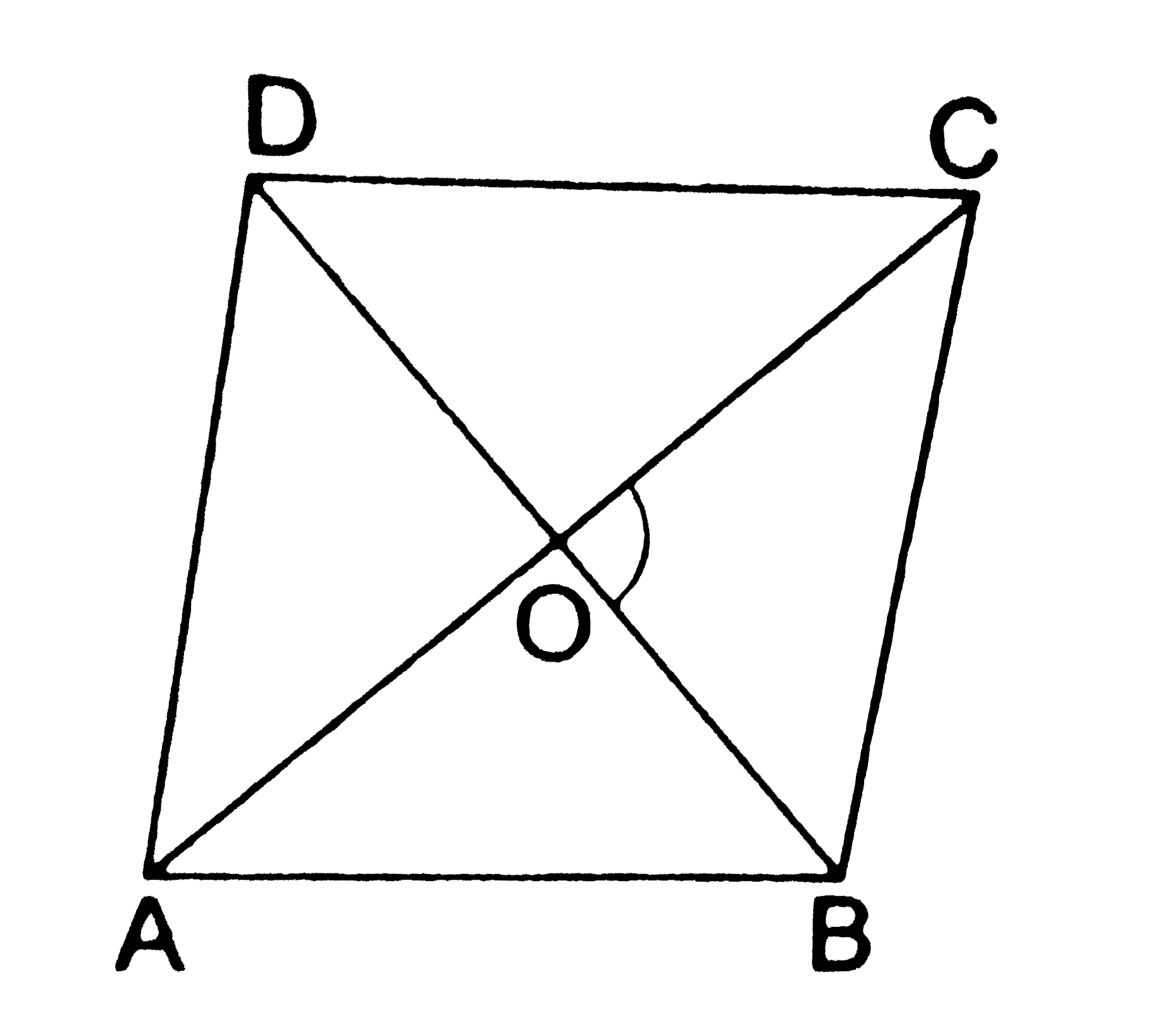
Prove that the circle drawn with any side of a rhombus as a diameter, posses through the point of intersection of its diagonals.
Let the diagonals AC and BD of a rhombus ABCD intersect at O. But, the diagonals of a rhombus bisect each other at right angles, So, ∠BOC=90∘
∴∠BOC lies in a semicircles.
Thus, the circle drawn with BC as diameter will pass through O. Similarly , all the circles described with AB, AD and CD as diameters , will pass through O.
Similar Questions
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point ofintersection of these circles lie on the third side
View SolutionIf two circles are drawn taking any two sides to the triangle as diameter then prove that point of intersection of two circles lies on the third side.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
View Solutionprove that the circle drawn on any focal distance as diameter touches the auxiliary circle in an ellipse
View SolutionIf the diagonals of a cyclic quadrilateral are perpendicular to each other, show that the line passing through the point of intersection of diagonals and midpoint of a side is perpendicular to the opposite side.
View SolutionProve that the tangent at any point of circle is perpendicular to the radius through the point of contact.
View SolutionProve that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base. Given: A ABC in which AB=AC and a circle is drawn by taking AB as diameter which intersects the side BC of triangle at D To Prove: BD=DC Construction : Join AD
View Solution

