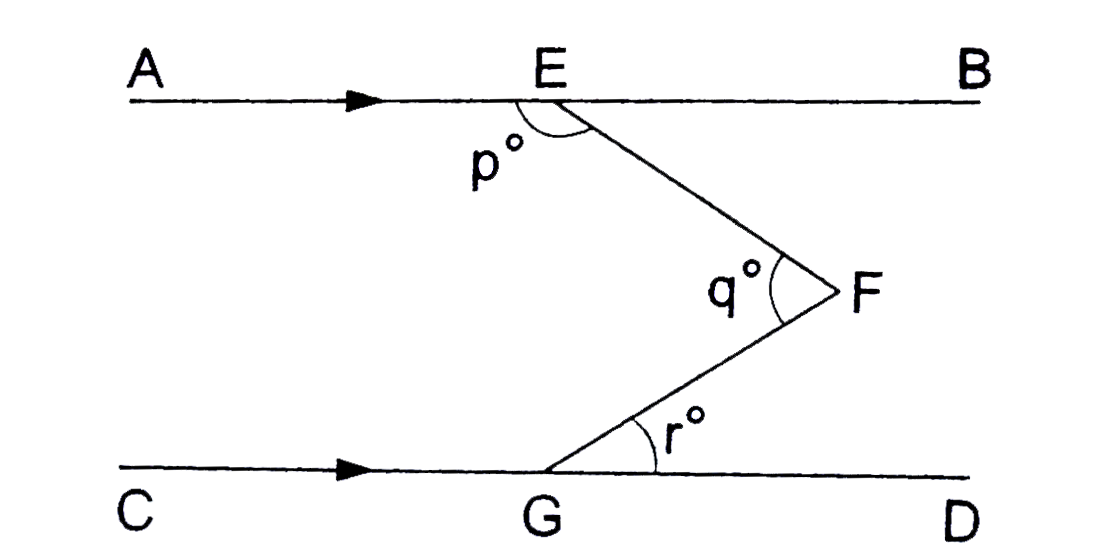
In the given figure, AB∣∣CD. Prove that ∠BAE−∠ECD=∠AEC

Video Solution
Text Solution
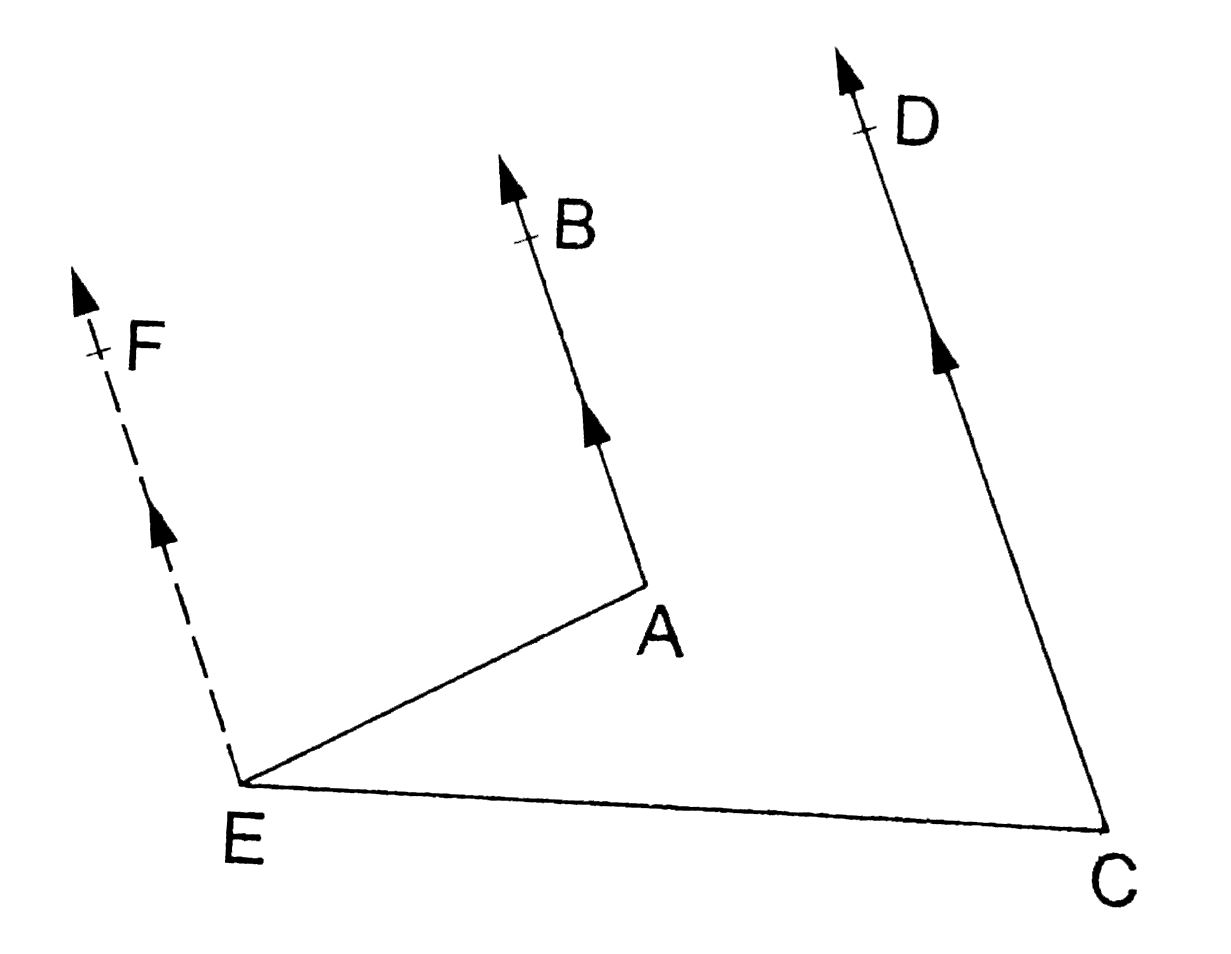
Through E, draw EF||AB||CD.
EF∣∣CD and EC is the transversal.
∴∠CEF+∠ECO=180∘.
AB∣∣EF and EC is the transversal.
∴∠CEF+∠ECD=180∘.
AB∣∣EF and EA is the transversal.
∴∠BAE+∠AEF=180∘
So, ∠CEF+∠ECD=∠BAE+∠AEF
⇒∠BAE−∠ECD=∠CEF−∠AEF=∠AEC.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure , AB∣∣CD. Find x.
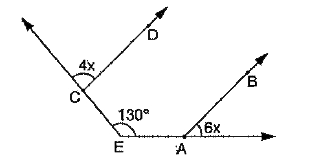 A26∘B13∘C23∘D46∘
A26∘B13∘C23∘D46∘ - Question 2 - Select One
In the figure, AB||CD then
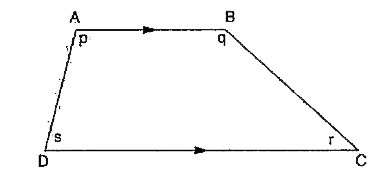 Ap+r=q+sBp−r=q−sCp+s=q+rDp−q=s−r
Ap+r=q+sBp−r=q−sCp+s=q+rDp−q=s−r
In the given figure , AB||CD . Prove that △AOB~△DOC.
 View Solution
View SolutionIn the given figure, AB∣∣CD. Prove that ∠BAE−∠ECD=∠AEC.
View SolutionIn the given figure, AB∣∣CD. Find the value of x.
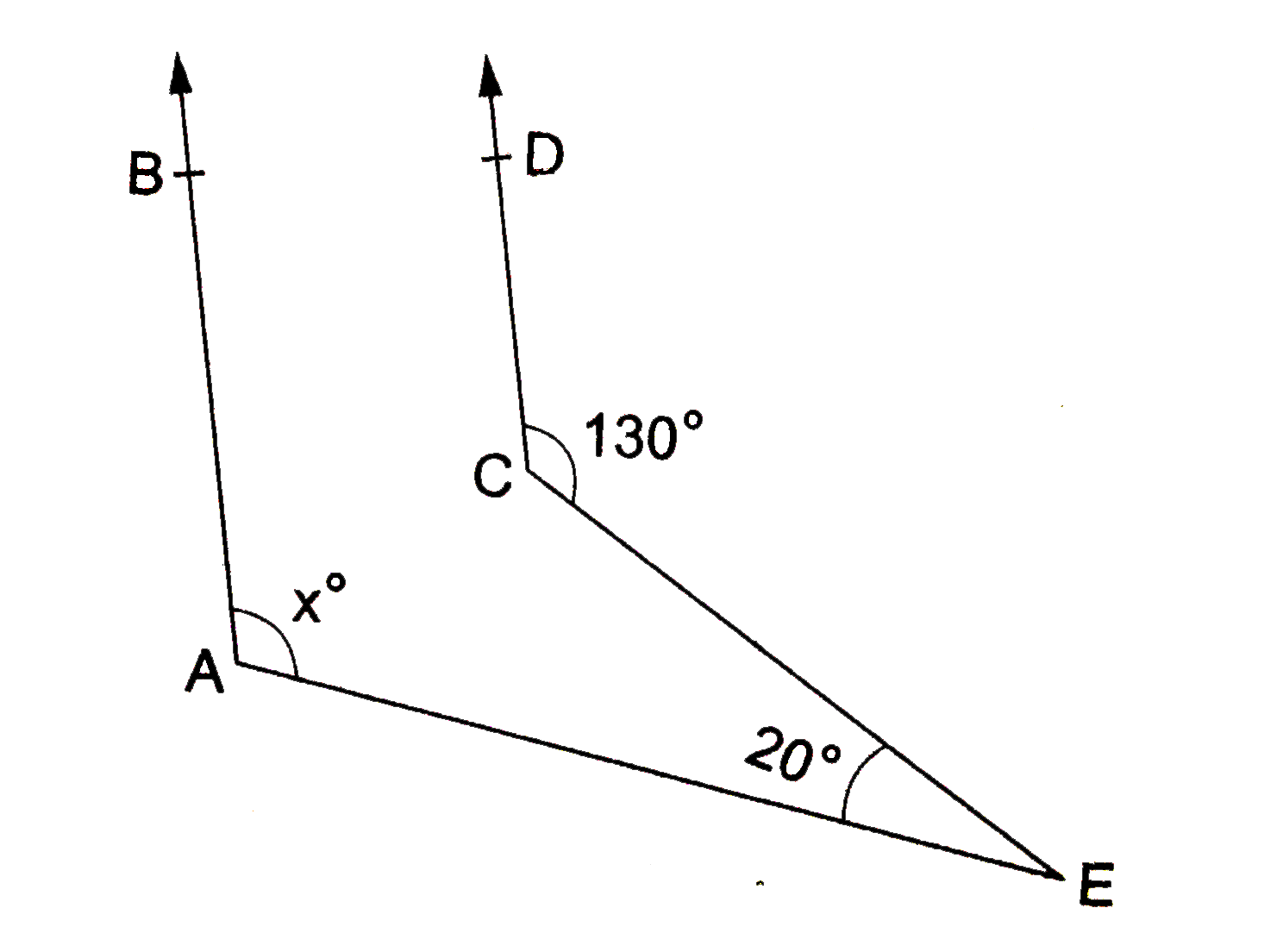 View Solution
View SolutionIn the given figure, AB∣∣CD. Find the value of x.
 View Solution
View SolutionIn the given figure, AB∣∣CD. Find the value of x.
 View Solution
View SolutionIn the given figure, AB∣∣CD,∠BAE=50∘,∠AEC=x∘ and ∠ECD=100∘. Find the value of x.
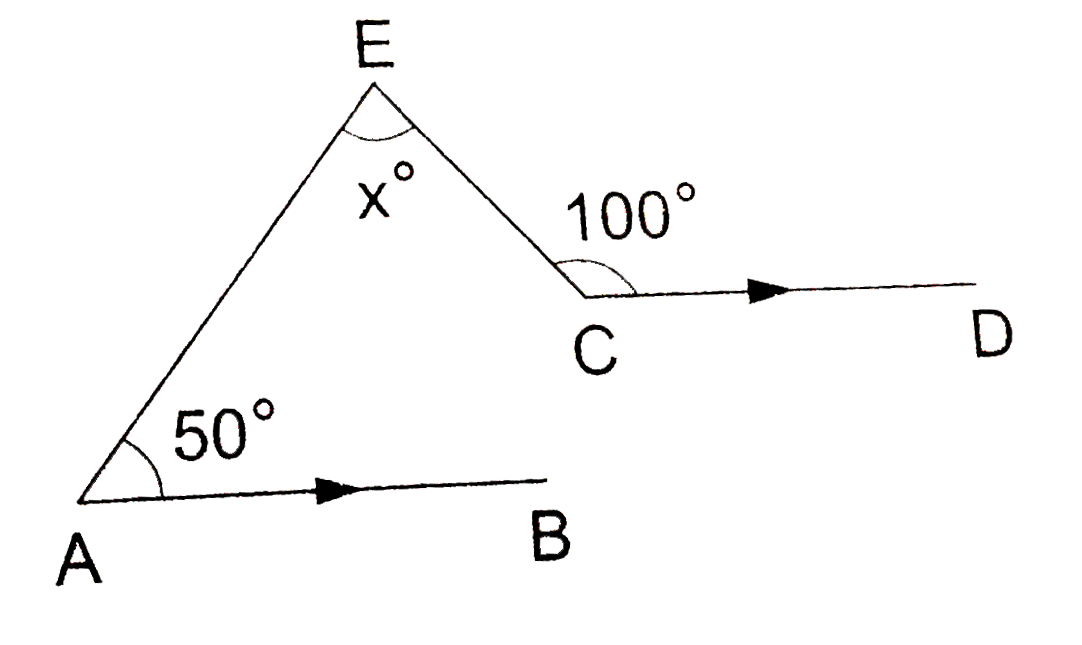 View Solution
View Solution