In the adjoining figure, ABCD is a quadrilateral and AC is one of its diagonals. Prove that
(i) AB+BC+CD+DA>2AC
(ii) AB+BC+CD>DA
(iii) AB+BC+CD+DA>AC+BD.
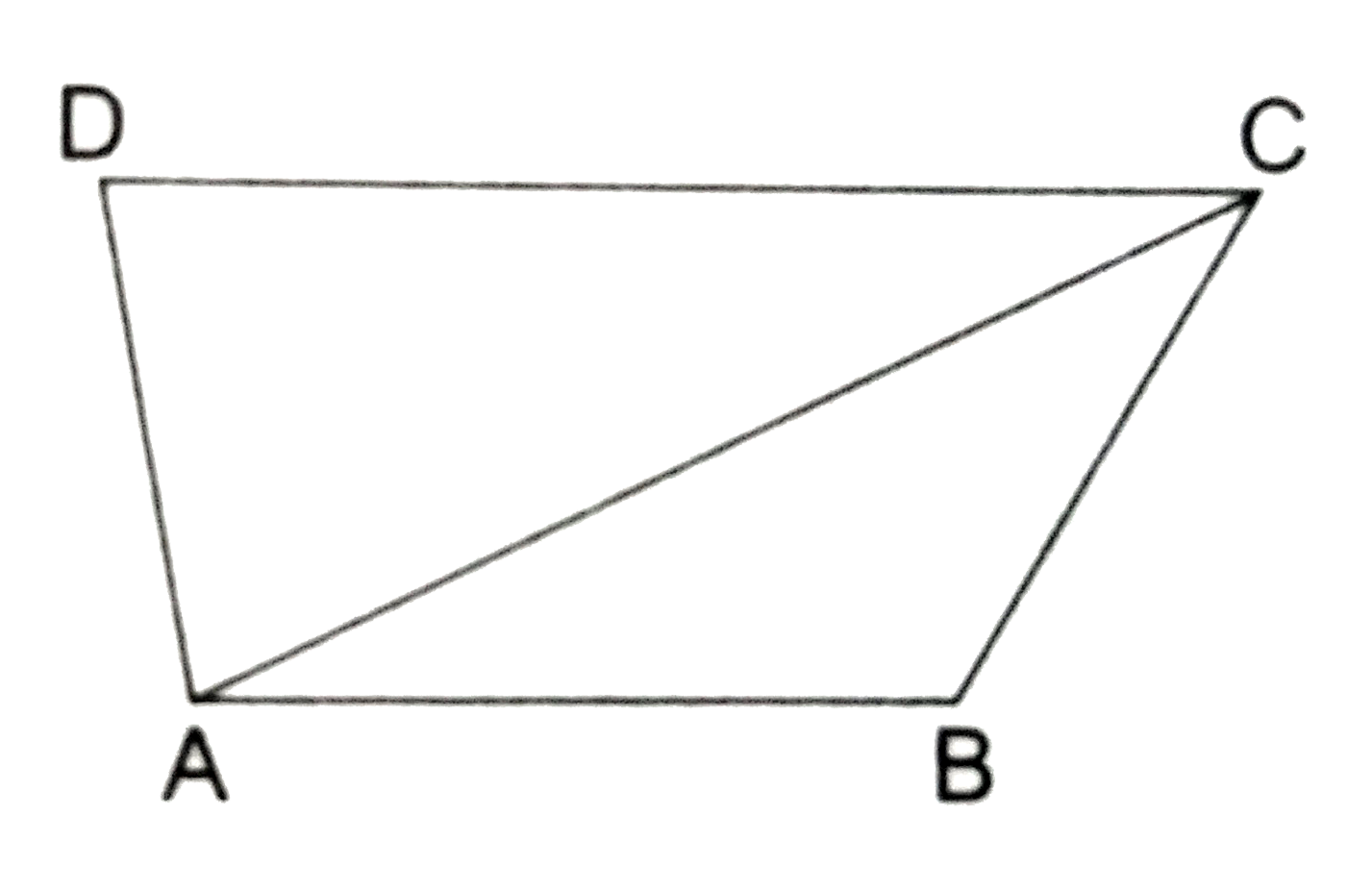
Step by step video & image solution for In the adjoining figure, ABCD is a quadrilateral and AC is one of its diagonals. Prove that (i) AB+BC+ CD+DA gt 2AC (ii) AB +BC+CD gt DA (iii) AB+BC+CD+DA gt AC+ BD. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
In the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)

View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
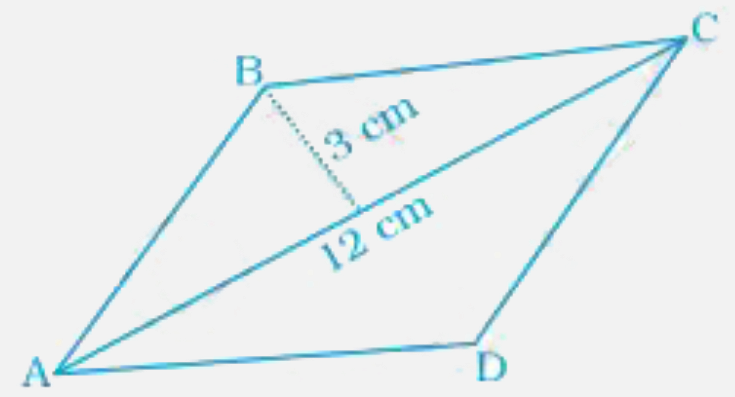
View SolutionABCD is a quadri,aterial prove that (AB+BC+CD+DA)>(AC+BD)

View SolutionIn the adjoining figure, x>y, Prove that AB>AC
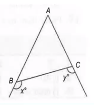
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
AB+CD=BC+AD.
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View SolutionThe given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD

View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View Solution
