Question

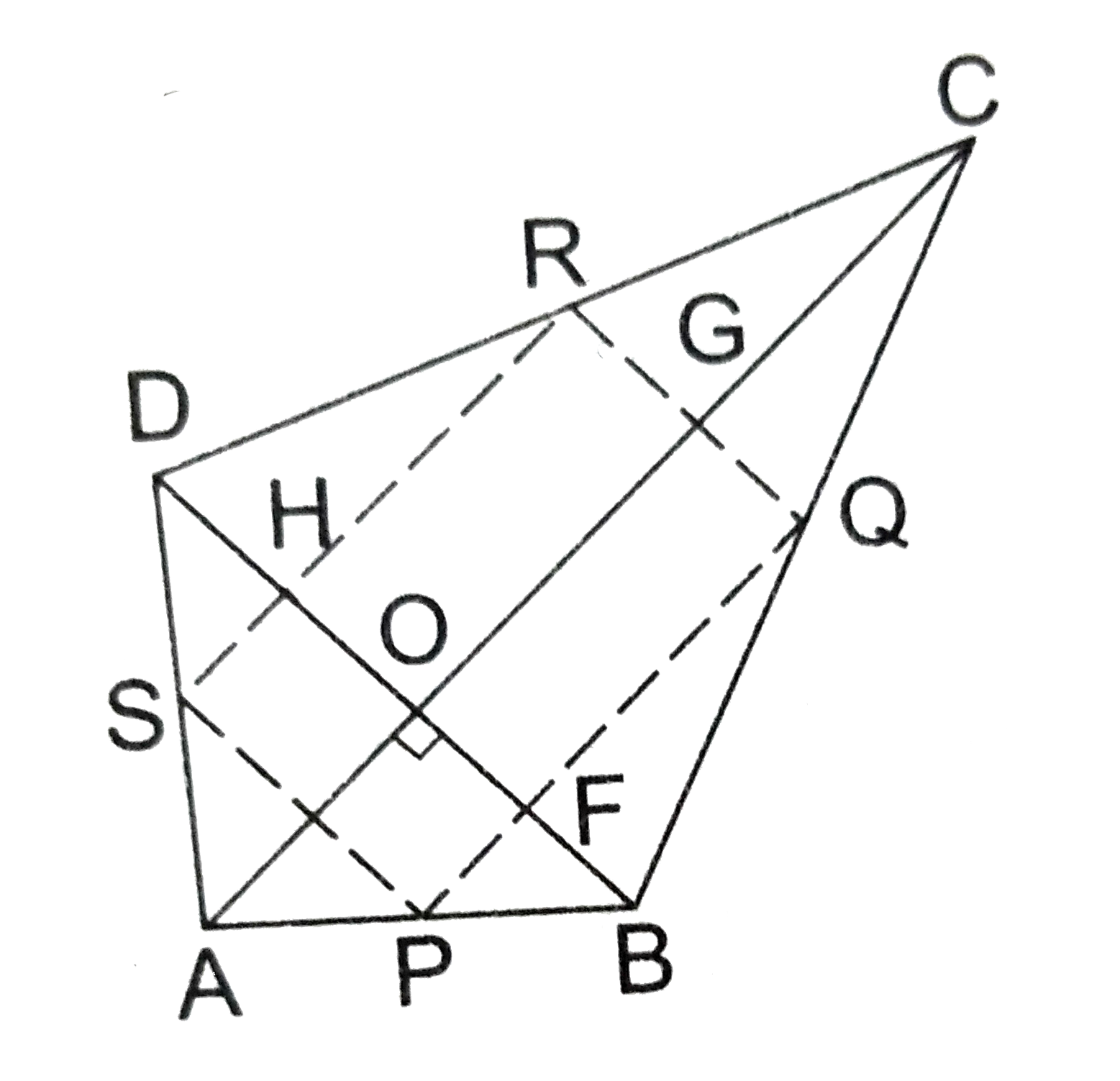
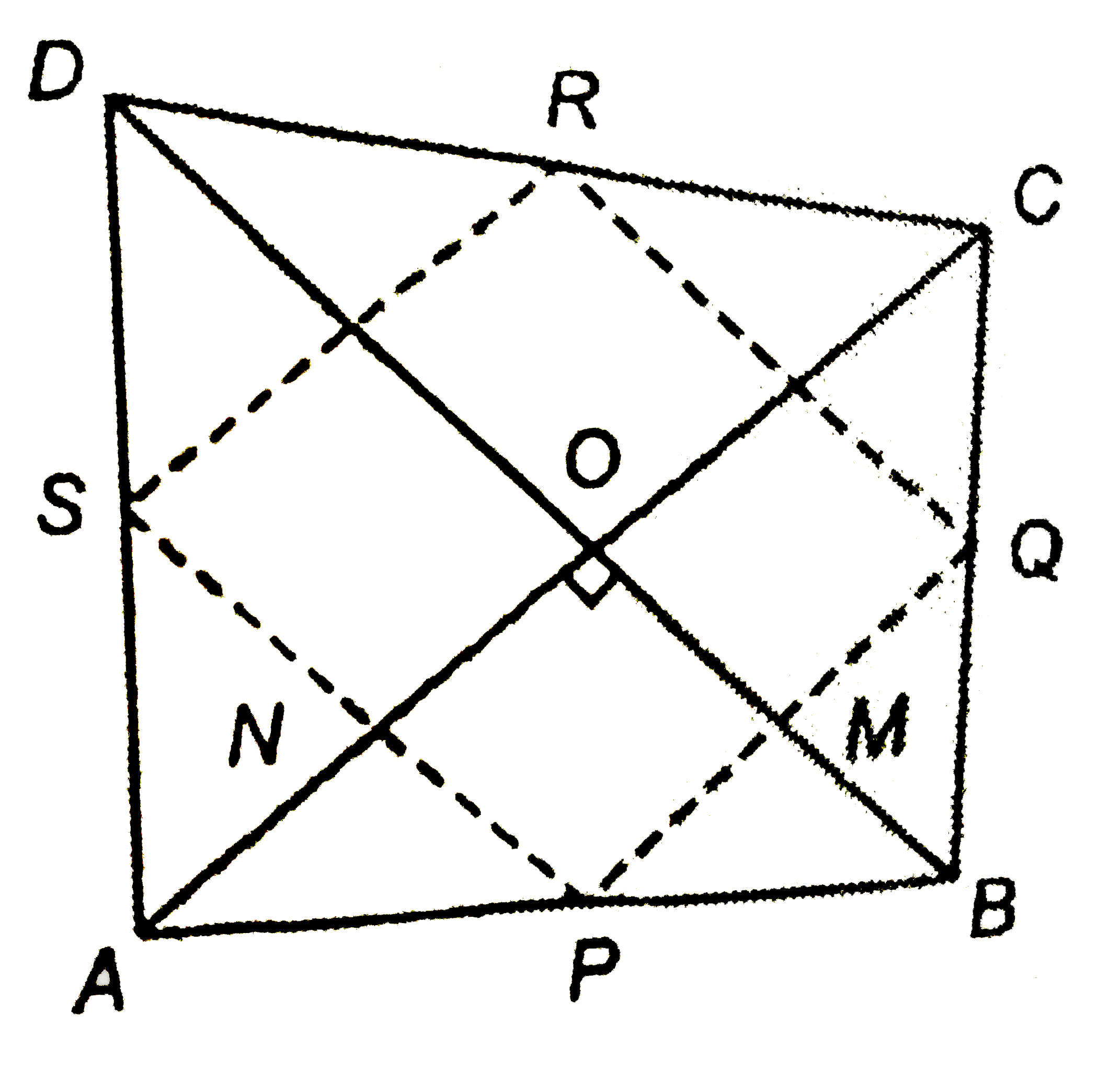
The diagonals of a quadrilateral $ABCD$
are perpendicular. Show that the quadrilateral, formed by joining the
mid-points of its sides, is a rectangle.

Explanation

P, Q, R and S are midpoints of sides AB, BC, CD and DA respectively.
`therefore ` PS||BD and PQ||AC
`rArr` PE||EO, i.e., EPFO is a ||gm.
And so, `angle EPF = angle EOF =90^(@), i.e., angle SPQ =90^(@).`
Now, PQRS is a ||gm with`angle SPQ =90^(@)`.
`therefore ` PQRS is a rectangle .