Over the past 200 working days , the number of defective parts produced by a machine is given in the following table :
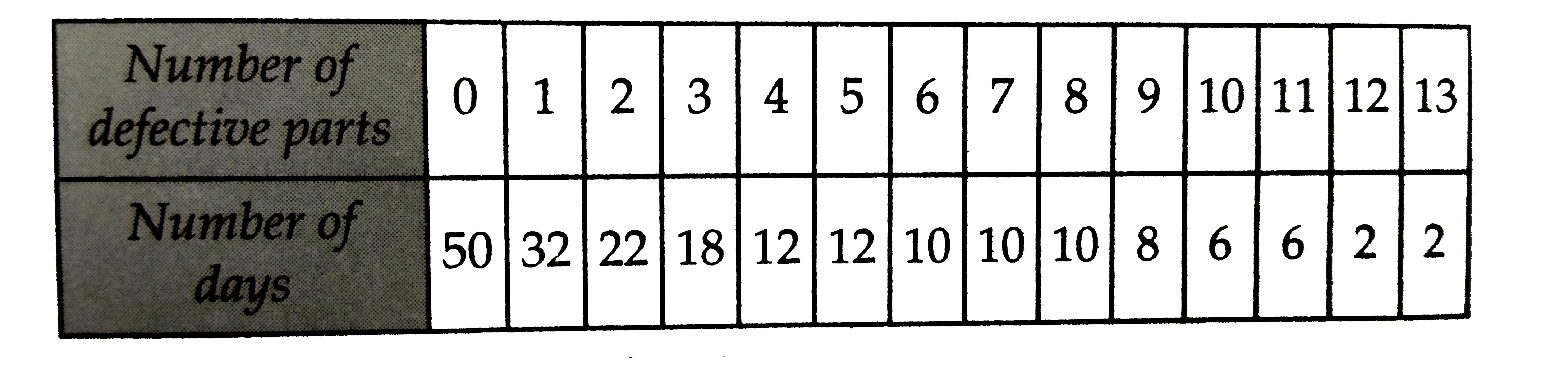
From these days , one day is chosen at random . What is the probability that on that day , the output has
(i) no defective part ?
(ii) at least 1 defective part ?
(iii) not more than 5 defective parts ?
(iv) more than 5 , but less than 8 defective parts ?
(v) more than 13 defective parts ?
Total number of working days = 200.
(i) Let E1 be the event that the output has 0 defective part on the chosen day . Then ,
P(event of producing 0 defective part on the chosen day)
=P(E1)
number of days when the output has 0 defective parttotal number of working days
=50200=14=0.25 .
(ii) Number of days on which the output has at least 1 defective part
= 200 - number of days with 0 defective part
= 200 - 50 = 150 .
Let E2 be the event that the output has at least 1 defective part on the chosen day . Then ,
P(E2)=150200=34.
(iii) Let E3 be the event that the output has not more than 5 defective parts , i.e., 5 or less defective parts , on the chosen day . Then ,
P(events that the output has not more than 5 defective parts on the chosen day)
= P (event that the output has 5 or less defective parts on the chosen day)
= P(E3)
=number of days when the output has 5 or less defective partstotal number of working days
=50+32+22+18+12+12200=146200=73100=0.73.
(iv) Let E4 be the event that the output has more than 5 , but less than 8 defective parts on the chosen day . Then ,
P (event that the output has more than 5 but less than 8 defective parts on the chosen day)
=P(E4)
=number of days when the output has 6 or 7 defective partstotal number of working days
=10+10200=20200=110=0.1.
(v) Let E5 be the event that the output has more than 13 defective parts on that day . then ,
P (event that the output has more than 13 defective parts on that day)
=P(E5)
=number of days when the output has more than 13 defective partstotal number of working days
=0200=0.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 1918videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - PRESENTATION OF DATA IN TABULAR FORMEXERCISE - Multiple Choice Questions (Mcq)9videos
PRESENTATION OF DATA IN TABULAR FORM
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
Similar Questions
Over the past 200 working days, the number of defective parts produced by a machine is given in the following table :
∣∣ ∣ ∣∣Number of0 1 2 3 4 5 6 7 8 9 10 11 12 13defective partsDays50 32 22 18 12 12 10 10 10 8 6 6 2 2∣∣ ∣ ∣∣
Determine the probability that tomorrow's output will have :
(i) no defective part.
(ii) at least one defective part,
(iii) not more than 5 defective parts,
(iv) more than 13 defective parts.View SolutionBulbs are packed in cartons , each containing 40 bulbs . 700 cartons were examined for defective bulbs and the results are given in the following table :

One carton is selected at random. What is the probability that it has
(i) no defective bulb?
(ii) defective bulbs less than 4 ?
(iii) defective bulbs more than 3 but less than 6 ?
(iv) defective bulbs 6 or more ?View Solution
Knowledge Check
- Question 1 - Select One
Over the past 200 working days, the number of defective parts produced by a machine is given is given in the followig table.
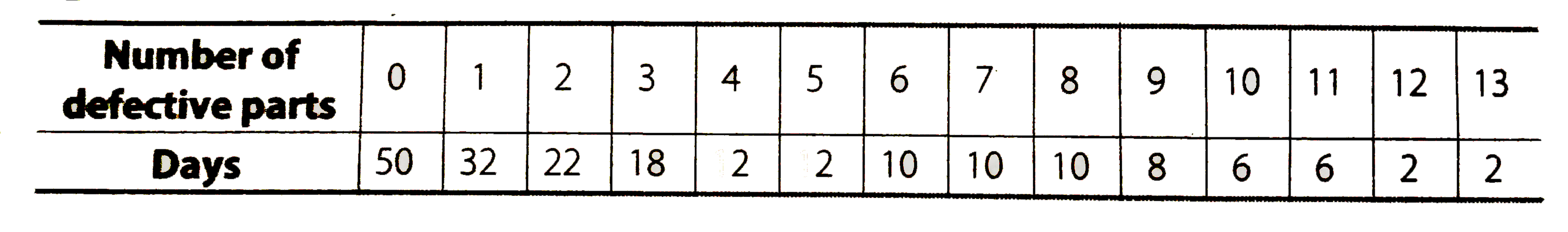
Determine the probability that tomorrow's output will haveAno defective part.Batleast one defective part.Cnor more than 5 defective parts.Dmore than 13 defective parts. - Question 2 - Select One
A box contains 5 defective and 15 non -defective bulbs two bulbs are chosen at random . Find the probability that both the bulbs are non - defective .
A519B320C2138Dnone of these
A lot of 20 eggs contains 5 defective eggs . One egg is drawn at random from the lot . What is the probability that
(i) This egg is defective ? (ii) This egg is not defective ?View SolutionIn a box containing 60 bulbs 6 are defective . What is the probability that out of a sample of 5 bulbs (i) none is defective (ii) exactly 2 are defective ?
View SolutionIn a box containing 100 bulbs, 10 are defective. What is the probability that out of a sample of 5 bulbs, (i) none is defective and (ii) exactly 2 are defective ?
View SolutionBulbs are packed in carbons each containing 40 bulbs, seven hundred cartons were examined for defective bulbs and the results are given in the following table.

One carton was selected at random. What is the probability that it has
i) no defective bulb?
ii) defective bulbs from 2-6?
iii) defective bulbs less than 4?View SolutionIn the items produced by a factory there are 10% defective items A sample of 6 items is randomly chosen . Find the probability that this sample contains (i) exactly 2 defective items (ii) not more than 2 defective items (iii) at least 3 defective items .
View SolutionIt is known that a box of 100 electric bulbs contains 8 defective bulbs. One bulb is taken out at random from the box. What is the probability that the bulb drawn is (i) defective? (ii) non -defective?
View Solution

