The graphical representation of the equations x+2y=3and2x+4y+7=0 gives a pair of
parallel lines
intersecting lines
coincident lines
none of these
The correct Answer is:A
To determine the nature of the pair of lines represented by the equations x+2y=3 and 2x+4y+7=0, we will follow these steps:
Step 1: Rewrite the equations in standard form
We need to express both equations in the form Ax+By+C=0.
1. For the first equation:
x+2y=3⟹x+2y−3=0
Here, A1=1, B1=2, and C1=−3.
2. For the second equation:
2x+4y+7=0
Here, A2=2, B2=4, and C2=7.
Step 2: Calculate the ratios A1A2, B1B2, and C1C2
Now, we will calculate the ratios of the coefficients:
1. Calculate A1A2:
A1A2=12
2. Calculate B1B2:
B1B2=24=12
3. Calculate C1C2:
C1C2=−37
Step 3: Analyze the ratios
We have:
- A1A2=12
- B1B2=12
- C1C2=−37
Step 4: Determine the nature of the lines
According to the conditions for the nature of lines:
- If A1A2=B1B2 but C1C2 is not equal to these ratios, the lines are parallel.
- If all three ratios are equal, the lines are coincident.
- If A1A2≠B1B2, the lines are intersecting.
In our case:
- A1A2=B1B2=12
- C1C2=−37 (not equal to 12)
Thus, the lines are parallel.
Final Answer
The graphical representation of the equations x+2y=3 and 2x+4y+7=0 gives a pair of parallel lines.
---
We need to express both equations in the form Ax+By+C=0.
x+2y=3⟹x+2y−3=0
Here, A1=1, B1=2, and C1=−3.
2x+4y+7=0
Here, A2=2, B2=4, and C2=7.
Now, we will calculate the ratios of the coefficients:
A1A2=12
B1B2=24=12
C1C2=−37
We have:
- A1A2=12
- B1B2=12
- C1C2=−37
According to the conditions for the nature of lines:
- If A1A2=B1B2 but C1C2 is not equal to these ratios, the lines are parallel.
- If all three ratios are equal, the lines are coincident.
- If A1A2≠B1B2, the lines are intersecting.
- A1A2=B1B2=12
- C1C2=−37 (not equal to 12)
The graphical representation of the equations x+2y=3 and 2x+4y+7=0 gives a pair of parallel lines.
Topper's Solved these Questions
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Multiple Choice Questions (Mcq)
27 Videos
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE BOOK - RS AGGARWALCHAPTER - MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
Show the graphical representation of given pair of linear equations x = 4 and y = 3.
A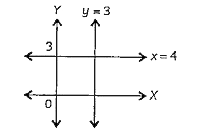 B
B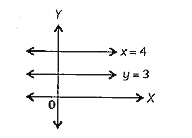 C
C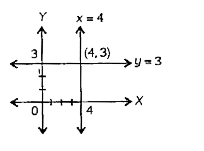 DNone of these
DNone of theseThe equations x + 2y + 3z = 1, x − y + 4z = 0 and 2x + y + 7z = 1has
Aonly one solutionBonly two solutionsCno solutionDinfinitely many solutionsGraphically, the pair of equations
6x−3y+10=0
2x−y+9=0
represents two lines which areAintersecting at exactly one pointBintersecting exactly two pointsCcoincidentDparallel
Solution of pair of linear equations x+2y=2andx−3y=7 is
View SolutionWhat is the value of k, for which the graphical representation of the simultaneous equations 5x−3y=1 and 2x−ky=−4 are parallel lines ?
View SolutionFind the solution of pair of linear equation x + 2y - 2 = 0 and x - 3y - 7 = 0.
View SolutionShow that the equation 2x2+xy−y2+x+4y−3=0 represents a pair of lines.
View SolutionSolve graphically the system of linear equations x+2y=3,4x+3y=2
View Solution
