Prove that tangent drawn at the mid point of the are of a circle is pallelar to the chord joing the ends of point of the are

Video Solution

Text Solution

Verified by Experts

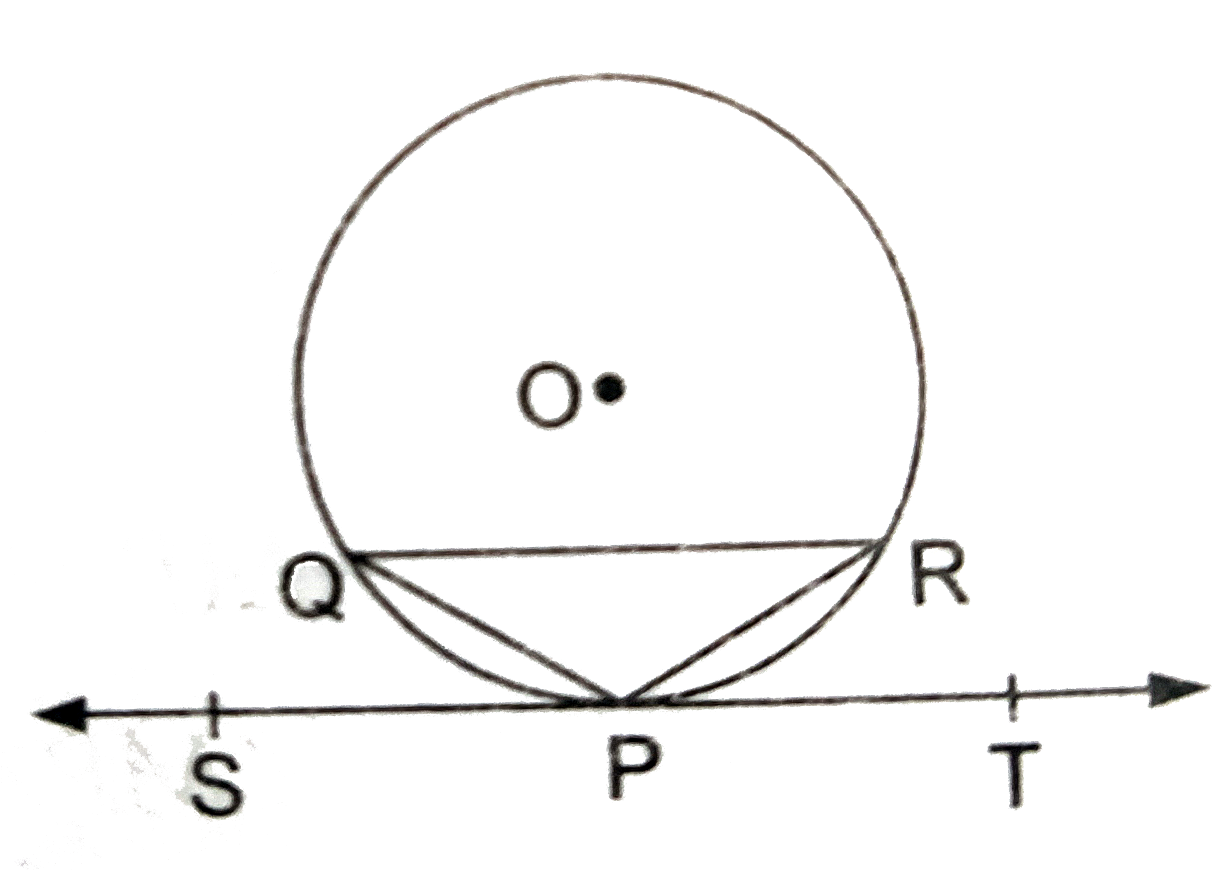
GIVEN Point $P$ is the midpoint of arc $ˆ Q R$ of a circle with centre $O$ . $S T$ is the tangent to the circle at point $P$ .
TO PROVE Chord $Q R ∣ ∣ S T$ .
PROOF $P$ is the midpoint of $ˆ Q R$
$\Rightarrow ˆ Q P = ˆ P R$
$\Rightarrow$ chord $Q P =$ chord $P R$ [ $∵$ in a cirlce, if two arcs are equal, then their corresponding chords are equal]
$∴ ∠ P Q R = ∠ P R Q$
$\Rightarrow ∠ T P R = ∠ P R Q$ [Note $∠ P Q R = ∠ T P R$ , angles in alternate segments]
$\Rightarrow Q R ∣ ∣ S T$ [ $∵ ∠ T P R$ and $∠ P R Q$ are alternate int.]

Updated on:21/07/2023

The tangents drawn at the end points of the diameter of a circle will be
Aperpendicular to each other
Bparallel to each other
Cinclined to each other at $45^{\circ}$
Dinclined to each other at $60^{\circ}$
Tangents drawn at the end points of a diameter are
APerpendicular
BParallel
CIntersecting
DNone of these
Number of tangents drawn from a point inside the circle is :
A1
B2
C4
D0