A quadrilateral ABCD is drawn to circumscribe a circle, as shown in the figure. Prove that AB+CD=AD+BC.
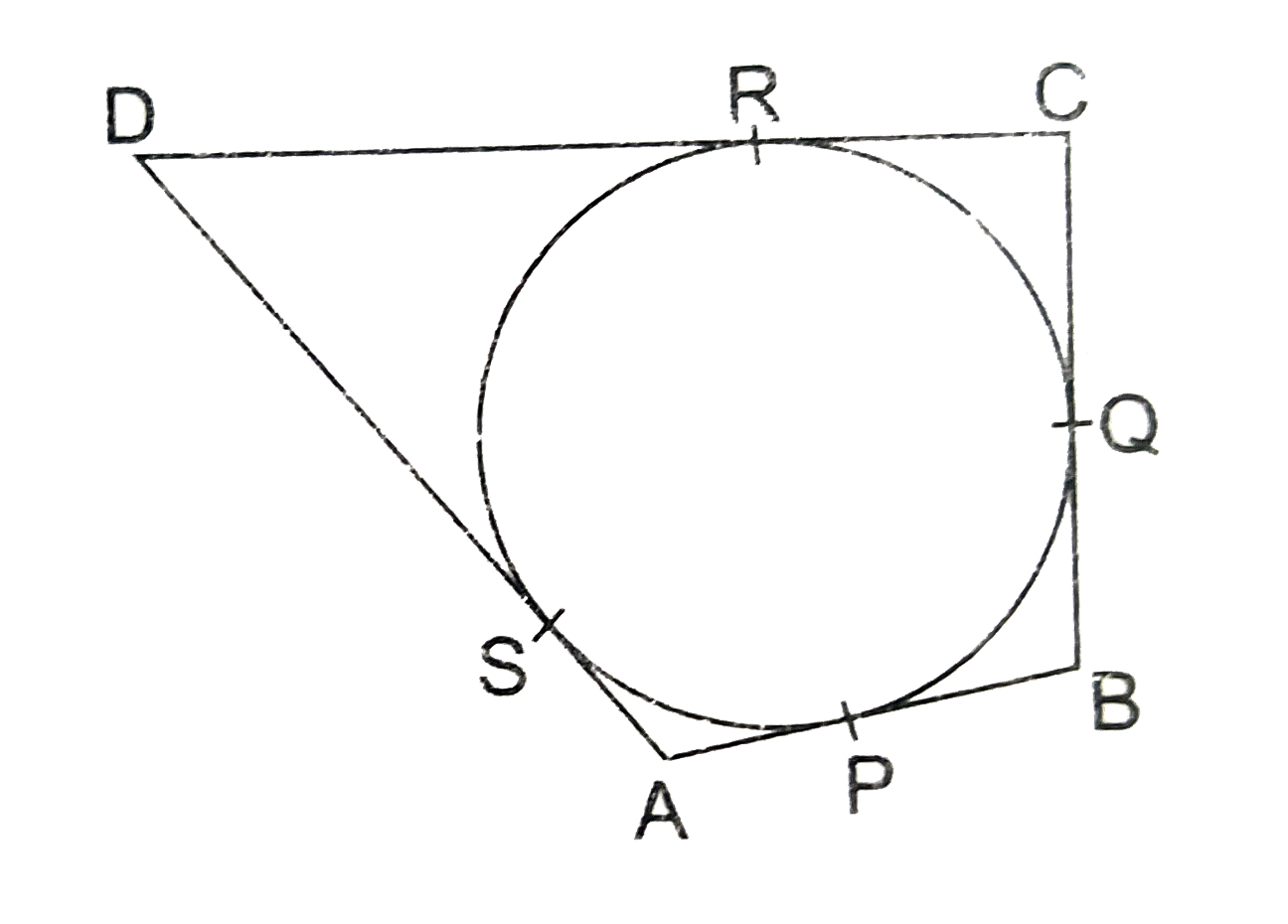
We know that the lengths of tangents drawn from an exterior point to a circle are equal.
∴AP=AS, ……..(i) [tangents from A]
BP=BQ, ……..(ii) [tangents from B]
CR=CQ, …….(iii) [tangents from C]
DR=DS, ……….(iv) [tangents from D]
∴AB+CD=(AP+BP)+(CR+DR)
=(AS+BQ)+(CQ+DS) [using (i), (ii), (iii), (iv)]
=(AS+DS)+(BQ+CQ)
=AD+BC.
Hence, AB+CD=AD+BC.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A16videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B15videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
A quadrilateral ABCD is drawn to circumscribe a circle such that its sides. AB , BC ,CD and DA touch the circle at P,Q,R and S , respectively . If AB = x cm BC = 7 cm , CR = 3 cm and AS = 5 cm , then x= ?
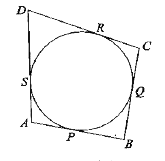 A10 cmB8 cmC9 cmD7 cm
A10 cmB8 cmC9 cmD7 cm - Question 2 - Select One
Quadrilateral ABCD is circumscribed to a circle. If AB=6cm, BC=7cm and CD=4cm then the length of AD is
A3cmB4cmC6cmD7cm - Question 3 - Select One
If the sides of a quadrilateral ABCD touch a circle and AB = 6 cm, CD = 5 cm, BC = 7 cm, then the length of AD in cm is :
A4 cmB5 cmC3 cmD6 cm
In Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionIn figure, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3cm and AS = 5cm, then x = ______.
 View Solution
View SolutionSides AB and CD of a quadrilateral ABCD are extended as shown in the figure Then a+b is equal to
 View Solution
View SolutionABCD is quadrilateral in which AD=BCand∠DAB=∠CBA (see figure). Prove that

BD=ACView Solution

