Show that the area of a triangle inscribed in an ellipse bears a constant ratio to the area of the triangle formed by joining points on the auxiliary circle correspoinding to the vertices of the first triangle.Solution in Telugu
Step by step video & image solution for Show that the area of a triangle inscribed in an ellipse bears a constant ratio to the area of the triangle formed by joining points on the auxiliary circle correspoinding to the vertices of the first triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELLIPSEBOOK - AAKASH SERIESCHAPTER - ELLIPSEEXERCISE - EXERCISE-I
52 Videos
- ELLIPSEBOOK - AAKASH SERIESCHAPTER - ELLIPSEEXERCISE - EXERCISE-II
68 Videos
- ELLIPSEBOOK - AAKASH SERIESCHAPTER - ELLIPSEEXERCISE - EXERCISE 4.3 (VERY SHORT ANSWER QUESTIONS)
4 Videos
- DIFFERENTIAL EQUATIONSBOOK - AAKASH SERIESCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Practice Exercise
62 Videos
- EXPONENTIAL SERIES BOOK - AAKASH SERIESCHAPTER - EXPONENTIAL SERIES EXERCISE - EXERCISE - III
8 Videos
Similar Questions
Focus (4, 0), e =12 , directrix is x -16 = 0. Then equation of the ellipse is
View SolutionFocus (3, 0), e =35, d irectrix 3x-25= 0, equation of the ellipse is
View SolutionIf p(θ) is a point on the ellipse x2a2+y2b2=1(a>b) then find its coresponding point
View SolutionThe degree and order of the differential equation [1+2(dydx)2]32=5d2ydx2 are
View Solution(1+3)loge3+1+322!(loge3)2+1+333!(loge3)3+.....∞ =
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View SolutionShow that the area of triangle inscribed in an ellipse bears a constant ratio to the area of thetriangle formed by joining points on the auxiliary circle corresponding to the vertices of the firsttriangle.
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View SolutionShow that the right triangle of maximum area that can be inscribed in a circle is an isosceles triangle
View SolutionA circle is inscribed ina n equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is
View SolutionA circle is inscribed in an equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is______
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
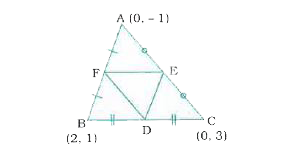
View SolutionFind the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are (0,-1), (2,1) and (0,3) . Find the ratio of this area to the area of the given triangle .
View SolutionShow that a triangle of maximum area that can be inscribed in a circle of radius a is an equilateral triangle.
View Solution
