Show that the area of a triangle inscribed in an ellipse bears a constant ratio to the area of the triangle formed by joining points on the auxillary circle correspoinding to the vertices of the first triangle.Solution in Telugu
Step by step video & image solution for Show that the area of a triangle inscribed in an ellipse bears a constant ratio to the area of the triangle formed by joining points on the auxillary circle correspoinding to the vertices of the first triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Show that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
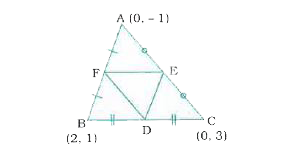
View SolutionFind the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are (0,-1), (2,1) and (0,3) . Find the ratio of this area to the area of the given triangle .
View SolutionShow that a triangle of maximum area that can be inscribed in a circle of radius a is an equilateral triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of the area of the triangle formed to the area of the given triangle
View SolutionIn a fort, there are 1200 soldiers. If each soldier consumes 3 kg per day, the provisions available in the fort will last for 30 days. If some more soldiers join, the provisions available will last for 25 days given each soldier consumes 2.5 kg per day. Find the number of soldiers joining the fort in that case ?
View SolutionShow that the area of triangle inscribed in an ellipse bears a constant ratio to the area of thetriangle formed by joining points on the auxiliary circle corresponding to the vertices of the firsttriangle.
View Solution
