For the one-dimensional motion, described by x = t - sintSolution in Gujrati
x(t)>0 for all t>0
v(t)>0 for allt>0
a(t)>0 for all t>0
v (t) lies between 0 and 2
The correct Answer is:A, B
Given, x=t−sint
velocity v=dxdt=ddt[t−sint]
=1−cost
Acceleration a=dvdt=ddt[1−cost]sint
As acceleration a>0 for all t>0(∵sint>0)
Hence,x(t)>0 for all t>0
Velocity v=1−cost
When, cost=1, velocity v=0
Vmax=1−(cost)min=1−(−1)=2
Vmin=1−(cost)max1−1=0
Hence, v lies between 0 and 2.
Acceleration a−dvdt=−sint
When t=0,x=0,v=+1,a=0
When t=90∘,x=1,v=0,a=−1
When t=180∘,x=0,v=−1,a=1
When t=360∘,x=0,v=0,a=0
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - SECTION-E71videos
MOTION IN A STRAIGHT LINE
- BOOK - KUMAR PRAKASHANCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - SECTION-F20videos
MOTION IN A STRAIGHT LINE
- BOOK - KUMAR PRAKASHANCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - SECTION-C43videos
MOTION IN A STRAIGHT LINE
- BOOK - KUMAR PRAKASHANCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - QUESTION PAPER (SECTION -C)3videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)5videos
OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE
Similar Questions
Velocity of a particle is given byv=(3t2+2t)ms. Find its average velocity between t = 0 to t=3s and also find its acceleration at t = 3s. Motion of the particle is in one dimension.
03:36View SolutionDistance covered by ball thrown upwards with speed 'u' in last 't' seconds before it reaches max. height is .............
06:47View SolutionWhat is acceleration ? What is the direction ? Also gives its unit.
04:01View SolutionGlycerine flows steadily through a horizontal tube of length 1.5m and radius 1.0 cm . If the amount of glycerine collected per second at one is 4.0×10−3kgs−1 , what is the pressure difference between the two ends of the tube ? (Density of glycerine =1.3×10103kgm−3 and viscosity of glycerine =0.83 Pa s). [ you may also like to check if the assumption of laminar flow in the tube is correct]
02:57View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere02:30View SolutionThe figure shows the position-time (x-t) graph of one-dimensional motion of a body of mass 0.4kg. The magnitude of each impulse is
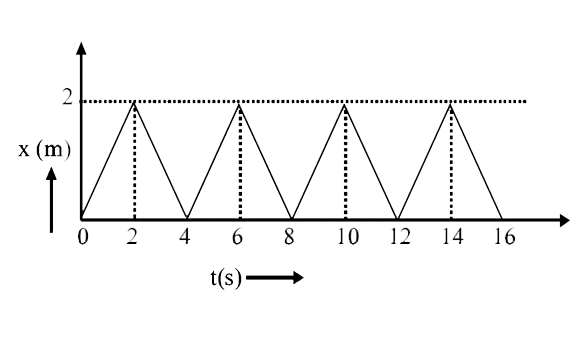 05:56View Solution
05:56View SolutionFor the one dimensional motion, described by x=t-sint
04:18View SolutionIn the one-dimensional motion of a particle, the relation between position x and time t is given by x2+2x=t (here x>0). Choose the correct statement.
05:41View Solutiondydx ज्ञात कीजिए -
x=et(sint+cost),y=et(sint−cost)05:25View Solutiondydx ज्ञात कीजिए -
x=a(cost+tsint),y=a(sint−tcost)04:04View Solutionयदि x=a(cost+tsint) और y=a(sint−tcost), तो d2ydx2 ज्ञात कीजिए ।
06:15View Solutionx = a (cost + t sint) , y = a (sint - tcost) find dydx .
05:58View SolutionSlope of the normal to the curvex=a(t+sint),y=a(t−sint) is
03:36View Solutionएकविमीय, द्विविमीय एवं त्रिविमीय गति छाँटिए- (iii ) वृत्तीय गति
09:04View Solutionयदि x=aet(sint−cost) तथा y=aet(sint+cost) तो dydx ज्ञात कीजिए।
02:42View Solution

