If O is the origin and the coordinates of A and B are (51, 65) and (75, 81), respectively. Then OA×OBcos∠AOB is equal to
The correct Answer is:9090
To solve the problem, we need to find the value of OA×OB×cos(∠AOB). Here are the steps to find the solution:
Step 1: Calculate the distances OA and OB
The distance OA can be calculated using the distance formula:
OA=√(xA−xO)2+(yA−yO)2
Given O(0,0) and A(51,65):
OA=√(51−0)2+(65−0)2=√512+652
Calculating 512 and 652:
512=2601and652=4225
Thus,
OA=√2601+4225=√6826
Now, calculate OB:
OB=√(xB−xO)2+(yB−yO)2
Given B(75,81):
OB=√(75−0)2+(81−0)2=√752+812
Calculating 752 and 812:
752=5625and812=6561
Thus,
OB=√5625+6561=√12186
Step 2: Calculate the distance AB
The distance AB can be calculated as:
AB=√(xB−xA)2+(yB−yA)2
AB=√(75−51)2+(81−65)2=√242+162
Calculating 242 and 162:
242=576and162=256
Thus,
AB=√576+256=√832
Step 3: Use the cosine rule to find cos(∠AOB)
According to the cosine rule:
AB2=OA2+OB2−2⋅OA⋅OB⋅cos(∠AOB)
Rearranging gives:
cos(∠AOB)=OA2+OB2−AB22⋅OA⋅OB
Step 4: Substitute the values
Now we substitute the values we calculated:
- OA2=6826
- OB2=12186
- AB2=832
Substituting into the cosine formula:
cos(∠AOB)=6826+12186−8322⋅√6826⋅√12186
Calculating the numerator:
6826+12186−832=18280
Step 5: Calculate OA×OB×cos(∠AOB)
Now we can find OA×OB×cos(∠AOB):
OA×OB×cos(∠AOB)=182802
Thus,
OA×OB×cos(∠AOB)=9140
Final Answer
The value of OA×OB×cos(∠AOB) is 9140.
OA=√(xA−xO)2+(yA−yO)2
Given O(0,0) and A(51,65):
OA=√(51−0)2+(65−0)2=√512+652
512=2601and652=4225
Thus,
OA=√2601+4225=√6826
OB=√(xB−xO)2+(yB−yO)2
Given B(75,81):
OB=√(75−0)2+(81−0)2=√752+812
752=5625and812=6561
Thus,
OB=√5625+6561=√12186
AB=√(xB−xA)2+(yB−yA)2
AB=√(75−51)2+(81−65)2=√242+162
242=576and162=256
Thus,
AB=√576+256=√832
AB2=OA2+OB2−2⋅OA⋅OB⋅cos(∠AOB)
Rearranging gives:
cos(∠AOB)=OA2+OB2−AB22⋅OA⋅OB
- OA2=6826
- OB2=12186
- AB2=832
cos(∠AOB)=6826+12186−8322⋅√6826⋅√12186
Calculating the numerator:
6826+12186−832=18280
OA×OB×cos(∠AOB)=182802
Thus,
OA×OB×cos(∠AOB)=9140
The value of OA×OB×cos(∠AOB) is 9140.
Topper's Solved these Questions
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (CONCEPT - BASED) SINGLE CORRECT ANSWER TYPE QUESTIONS
15 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (LEVEL 1) SINGLE CORRECT ANSWER TYPE QUESTIONS
60 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - SOLVED EXAMPLES (LEVEL 2) SINGLE CORRECT ANSWER TYPE QUESTIONS
30 Videos
- AREA BY INTEGRATIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - AREA BY INTEGRATIONEXERCISE - Question from Previous Years. B-Architecture Entrance Examination Papers
12 Videos
- CIRCLES AND SYSTEMS OF CIRCLES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
17 Videos
Similar Questions
Knowledge Check
In given triangle ABC ,OB and OC are bisectors of ∠Ba nd ∠C respectively then ∠BOC is equal to
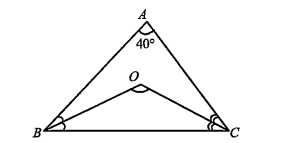 A70∘B110∘C140∘D80∘
A70∘B110∘C140∘D80∘If two points A and B lie on the curve y=x2 such that −−→OA.ˆi=1and−−→OB.ˆj=4, where O is origin and A and B lie in the 1st and 2nd quadrant respectively, then −−→OA.−−→OB is equal to
A0B2C4D5If in a ΔABC, O and O' are the incentre and orthocentre respectively, then (O'A+O'B+O'C) is equal to
A2O'OBO'OCOO'D2OO'
If in a ΔABC, O and O' are the incentre and orthocentre respectively, then (O'A+O'B+O'C) is equal to
View SolutionThree particles each 1kg mass are placed at the corners of a right angled triangle AOB, O being the origin of the co-ordinate system OA and OB along +ve x-direction and +ve y-direction. The position vector of the centre of mass is (OA=OB=1m) (in meters)
View SolutionThe tangent at an extremity (in the first quadrant) of latus rectum of the hyperbola x24−y25=1 meets x-axis and y- axis at A and B respectively. Then (OA)2−(OB)2, where O is the origin, equal to
View SolutionIf the bisector of the angles A and B of a quadrilateral ABCD meet at O, then ∠AOB is equal to:
View SolutionTwo circular path of radii a and b intersect at a point O and AB is a line through O meeting the circles at A and B respectively. Chords OA and OB subtend equal angles of 60∘ at their respective centres. A vertical pole at O subtends angles αandβ respectively at A and B then height of the pole is
View Solution
