ABCD is a rectangle in the clockwise direction. The coordinates of A are (1, 3) and of C are (5, 1), vertices B and D lie on the line y=2x+c, then the coordinates of D are
(2, 0)
(4, 4)
(0, 2)
(2, 4)
The correct Answer is:A
To find the coordinates of point D in rectangle ABCD, we will follow these steps:
Step 1: Identify the coordinates of points A and C
Given:
- A = (1, 3)
- C = (5, 1)
Step 2: Find the midpoint of diagonal AC
The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by the formula:
M=(x1+x22,y1+y22)
For points A and C:
MAC=(1+52,3+12)=(62,42)=(3,2)
Step 3: Use the midpoint property of the rectangle
Since the diagonals of a rectangle bisect each other, the midpoint of diagonal BD will also be (3, 2).
Let the coordinates of points B and D be (x1, y1) and (x2, y2) respectively. Therefore, we have:
x1+x22=3andy1+y22=2
From these equations, we can derive:
x1+x2=6(1)
y1+y2=4(2)
Step 4: Use the line equation for BD
We know that points B and D lie on the line given by:
y=2x+c
From the midpoint property, we can express y1 and y2 in terms of x1 and x2:
y1=2x1+c(3)
y2=2x2+c(4)
Step 5: Substitute equations (3) and (4) into equation (2)
Substituting (3) and (4) into (2):
(2x1+c)+(2x2+c)=4
This simplifies to:
2x1+2x2+2c=4
Using equation (1) (where x1+x2=6):
2(6)+2c=4
12+2c=4
2c=4−12
2c=−8⇒c=−4
Step 6: Substitute c back into equations for y1 and y2
Now substituting c back into equations (3) and (4):
y1=2x1−4(5)
y2=2x2−4(6)
Step 7: Substitute equations (5) and (6) into equation (2)
Substituting (5) and (6) into (2):
(2x1−4)+(2x2−4)=4
This simplifies to:
2x1+2x2−8=4
Using equation (1):
2(6)−8=4
This is consistent.
Step 8: Find coordinates of D
Now, we can solve for x1 and x2 using equations (1), (5), and (6). We can express x2 in terms of x1:
x2=6−x1
Substituting into equation (6):
y2=2(6−x1)−4=12−2x1−4=8−2x1
Now we have:
- y1=2x1−4
- y2=8−2x1
Setting y1=y2:
2x1−4=8−2x1
4x1=12⇒x1=3
Then:
x2=6−3=3
Substituting x1 back into (5) to find y1:
y1=2(3)−4=2
And substituting x2 back into (6) to find y2:
y2=8−2(3)=2
Thus, the coordinates of point D are:
D=(2,0)
Final Answer:
The coordinates of D are (2, 0).
---
Given:
- A = (1, 3)
- C = (5, 1)
The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by the formula:
M=(x1+x22,y1+y22)
MAC=(1+52,3+12)=(62,42)=(3,2)
Since the diagonals of a rectangle bisect each other, the midpoint of diagonal BD will also be (3, 2).
x1+x22=3andy1+y22=2
From these equations, we can derive:
x1+x2=6(1)
y1+y2=4(2)
We know that points B and D lie on the line given by:
y=2x+c
y1=2x1+c(3)
y2=2x2+c(4)
Substituting (3) and (4) into (2):
(2x1+c)+(2x2+c)=4
This simplifies to:
2x1+2x2+2c=4
Using equation (1) (where x1+x2=6):
2(6)+2c=4
12+2c=4
2c=4−12
2c=−8⇒c=−4
Now substituting c back into equations (3) and (4):
y1=2x1−4(5)
y2=2x2−4(6)
Substituting (5) and (6) into (2):
(2x1−4)+(2x2−4)=4
This simplifies to:
2x1+2x2−8=4
Using equation (1):
2(6)−8=4
This is consistent.
Now, we can solve for x1 and x2 using equations (1), (5), and (6). We can express x2 in terms of x1:
x2=6−x1
Substituting into equation (6):
y2=2(6−x1)−4=12−2x1−4=8−2x1
- y1=2x1−4
- y2=8−2x1
2x1−4=8−2x1
4x1=12⇒x1=3
Then:
x2=6−3=3
Substituting x1 back into (5) to find y1:
y1=2(3)−4=2
And substituting x2 back into (6) to find y2:
y2=8−2(3)=2
D=(2,0)
The coordinates of D are (2, 0).
Topper's Solved these Questions
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (LEVEL 2) SINGLE CORRECT ANSWER TYPE QUESTIONS21videos
CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (NUMERICAL ANSWER TYPE QUESTIONS)21videos
CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (CONCEPT - BASED) SINGLE CORRECT ANSWER TYPE QUESTIONS15videos
CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - AREA BY INTEGRATIONEXERCISE - Question from Previous Years. B-Architecture Entrance Examination Papers12videos
AREA BY INTEGRATION
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS17videos
CIRCLES AND SYSTEMS OF CIRCLES
Similar Questions
ABCD is a rectangle in the clock-wise direction. The co-ordinates of A are (1,3)and of C are (5,1) vertices B and D lie on line y=2x+c. The co-ordinate of the
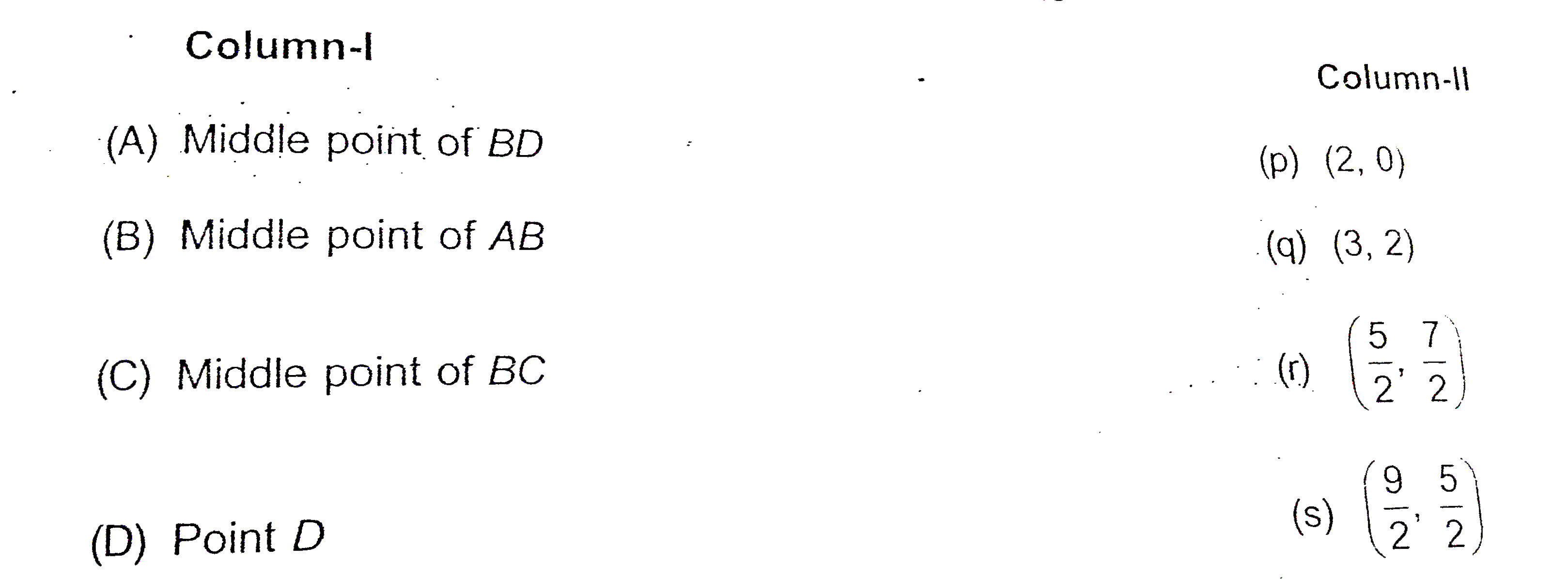 View Solution
View SolutionThe area of triangle ABC is 20cm2. The coordinates of vertex A are −5,0) and those of B are (3,0). The vertex C lies on the line x−y=2 . The coordinates of C are (5,3) (b) (−3,−5) (−5,−7) (d) (7,5)
View Solution
Knowledge Check
- Question 1 - Select One
If A(4, 2), B(6, 5) and C(1, 4) be the vertices of ΔABC and AD is a median, then the coordinates of D are
A(52,3)B(5,72)C(72,92)Dnone of these - Question 2 - Select One
A rectangle has two opposite vertices at the points (1,2) and (5,5). If the other vertices lie on the line x=3, then their coordinates are
A(3,1), (3,3)B(3,1), (3,6)C(3,1),(3,4)Dnone of these - Question 3 - Select One or More
A(1, 3) and C(5, 1) are two opposite vertices of a rectangle ABCD. If the slope of BD is 2, then the coordinates of B can be :
A(4, 4)B(5, 4)C(2, 0)D(1, 0)
ABCD is parallelogram. If the coordinates of A,B,C are (−2,−1),(3,0) and (1,−2) respectively, find the coordinates of D.
View SolutionIf A( 1,2) , B( 4,3) and C ( 0,0) are three vertices of parallelogram ABCD , find the coordinates of D.
View SolutionA(1, 3) and C(5, 1) are two opposite vertices of a rectangle ABCD. If the slope of BD is 2, then the coordinates of B can be :
View SolutionIf A (1,0), B (5,3), C(2,7) and D (x, y) are vertices of a parallelogram ABCD, the co-ordinates of D are
View SolutionThe points (1,3)and(5,1) are the opposite vertices of a rectangle. The other two vartices lie on the line y=2x+c, then the value of c will be
View Solution

