If A,B,C,D are four points in space satisfying ¯¯¯¯¯¯AB.¯¯¯¯¯¯CD=K[∣∣¯¯¯¯¯¯AD∣∣2+∣∣¯¯¯¯¯¯BC∣∣2−|AC|2−|BD|2] then the value of K is
2
1/3
1/2
1
The correct Answer is:C
Step by step video, text & image solution for If A, B, C, D are four points in space satisfying bar(AB).bar(CD)=K [|bar (AD)|^2+|bar (BC)|^2-|AC|^2-|BD|^2] then the value of K is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR ALGEBRABOOK - MCGROW HILL PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLVED EXAMPLES (Level-2 Single Correct Answer Type Questions)
25 Videos
- VECTOR ALGEBRABOOK - MCGROW HILL PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLVED EXAMPLES (Numerical Answer Type Questions)
25 Videos
- VECTOR ALGEBRABOOK - MCGROW HILL PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLVED EXAMPLES (Concept -Based Single Correct Answer Type Questions)
10 Videos
- TRIGONOMETRICAL IDENTITIES AND EQUATIONS BOOK - MCGROW HILL PUBLICATIONCHAPTER - TRIGONOMETRICAL IDENTITIES AND EQUATIONS EXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
20 Videos
Similar Questions
Knowledge Check
If ABCD is a square then,
2¯¯¯¯¯¯AB+4¯¯¯¯¯¯BC+5¯¯¯¯¯¯CD+7¯¯¯¯¯¯DA=A2¯¯¯¯¯¯BDB3¯¯¯¯¯¯CAC5¯¯¯¯¯¯DBD2¯¯¯¯¯¯ACIf ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =A4 ¯¯¯¯¯¯ACB3 ¯¯¯¯¯¯ACC2 ¯¯¯¯¯¯CAD¯¯¯¯¯¯ACIf D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
A2(¯¯¯¯¯¯AD−¯¯¯¯¯¯BD)B2(¯¯¯¯¯¯DC−¯¯¯¯¯¯BD)C2(¯¯¯¯¯¯BD−¯¯¯¯¯¯CA)D2(¯¯¯¯¯¯BD−¯¯¯¯¯¯AC)
If A, B, C and D are four non-collinear points in the plane such that ¯¯¯¯¯¯AD+¯¯¯¯¯¯BD+¯¯¯¯¯¯CD=¯0, then prove that the points D is the centroid of the triangle ABC.
View SolutionIf A,B,C and D are four points and ¯¯¯¯¯¯AB=¯¯¯¯¯¯DC then ¯¯¯¯¯¯AC+¯¯¯¯¯¯BD= (A) 2−−→AD (B) 2−−→CB (C) 2−−→AC (D) none
View SolutionIf A,B,C,D are four distinct point in space such that AB is not perpendicular to CD and satisfies →AB.→CD=k(∣∣→AD∣∣2+∣∣→BC∣∣2−∣∣→AC∣∣2−∣∣→BD∣∣2), then find the value of k.
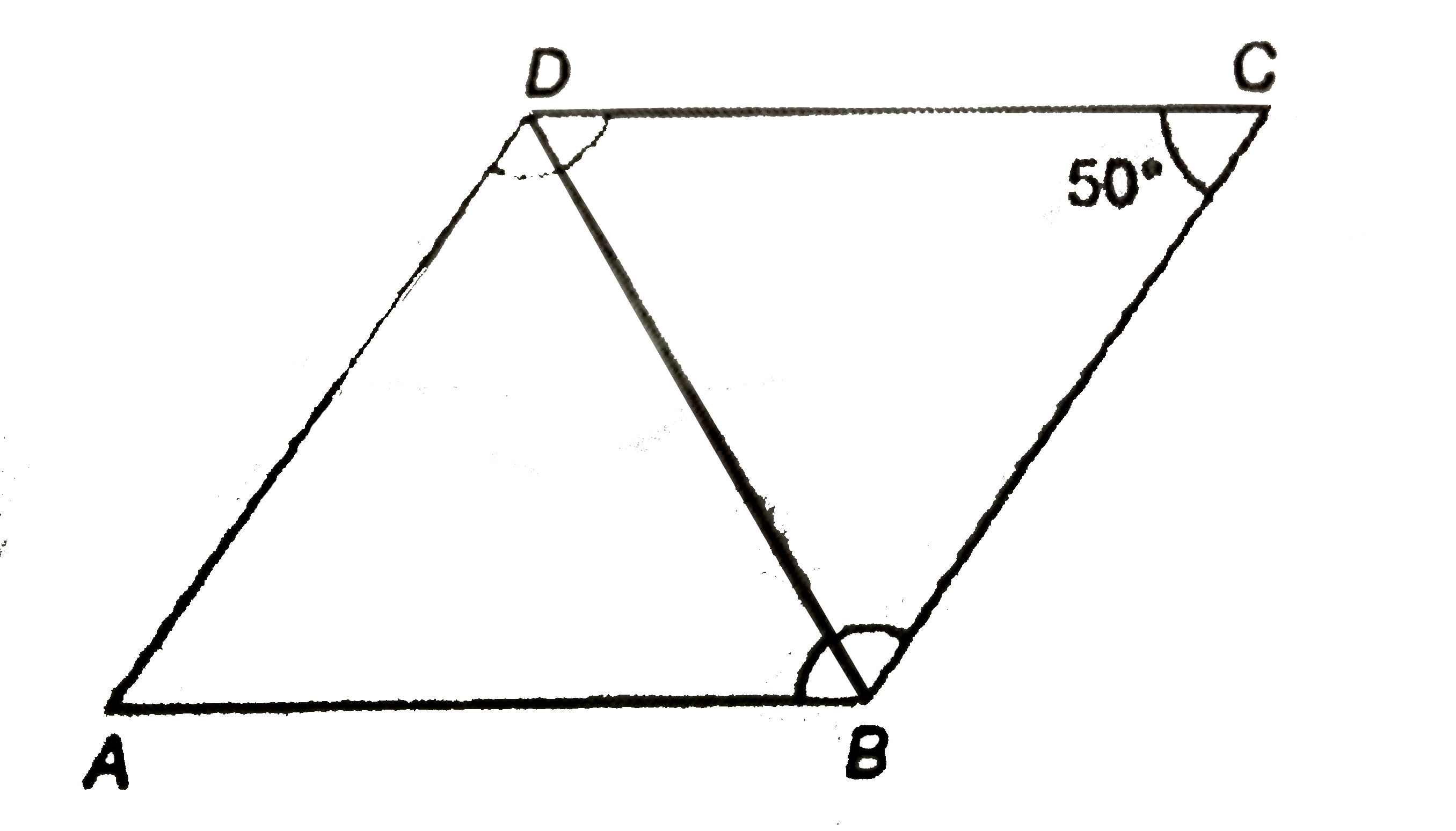
View SolutionIn the figure, ABD, BCD are two triangles. BD is the bisector of ∠ABCand∠ADC.¯¯¯¯¯¯AB || ¯¯¯¯¯¯CDand¯¯¯¯¯¯AD || ¯¯¯¯¯¯BC. If ∠BCD=50∘, then find the angle of ∠BAD.
View SolutionIf ¯a,¯b,¯c,¯d are position vectors of the points A,B,CandD respectively in three dimensional space and satisfy the relation 3¯a−2¯b+¯c−2¯d=0 .Then which of the following is incorrect
View Solution
