For a chemical reaction aA→B,log[−d[A]dt]=log[d[B]dt]+0.3 then find the approximate ratio and of a and bSolution in Telugu
The correct Answer is:2
aA→bB−d[A]dt=_d[B]dt×(ab)
log(dAdt)=log(dBdt)+log(ab) So log(ab)=0.3=log2,ab=2
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - PRACTICE SHEET-1 (SINGLE OR MORE THAN ONE OPTION QUESTIONS)16videos
CHEMICAL KINETICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - PRACTICE SHEET-1 (LINKED COMPREHENSION TYPE QUESTIONS)6videos
CHEMICAL KINETICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - LEVEL-II(LECTURE SHEET EXERCISE-III MATCH THE FOLLOWING QUESTIONS)3videos
CHEMICAL KINETICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETCSEXERCISE - EXERCISE - 3.245videos
CHEMICAL KINETCS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL THERMODYNAMICSEXERCISE - Additional Practice Exercise54videos
CHEMICAL THERMODYNAMICS
Similar Questions
For the reaction N2+3H2→2NH3 , the rate d[NH3]dt=2×10−4Ms−1. Therfore the rate −d[N2]dt is given
00:42View SolutionThe instantaneous rate of an elementary chamical reactkon aA+bB⇔cC+dD can be given by rate =Kf[A]a[B]b−Kb[C]c[D]d where Kf and Kb are rate constants for forward and backward reactions respectively for the reversible reaction. If the reaction is an irreversible one, the rate is expressed as, rate =K[A]a[B]b where K is rate contant for the given irreversible rate of disappearance of A is a/b times the rate of disappearance of B. The variation of rate constant K with temperature is expressed in terms of Arrhenius equation: K=Ae−Ea/RT whereas the ratio KfKb is expressed in terms of van't Hoff isochore: KfKb=Ae−ΔH/RT, where Ea and ΔH are energy of activation and heat of reaction respectively.
The variation of rate constant K and KfKb with temperature shows the following effects:
For endothrmic reaction when T increases then K increases and KfKb also increases.
(ii) For endothemic reaction when T decreases then K decreases and KfKb also decreases.
(iii) For exothermic when T increases then K and KfKb both increases.
(iv) For exothermic reaction when T decreases then K increases and KfKb decrease.
(v) For exothermic reaction when T increases thenK and KfKb both decrease.02:01View SolutionMatch the following columns
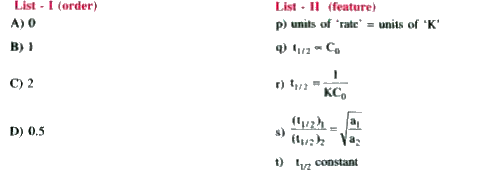 14:30View Solution
14:30View SolutionDiscuss on the kinetic spontaneity of a chemical reaction. Is a slow reaction spontaneous? Why?
02:51View SolutionWhich among the following is not an exact differential?
04:46View Solution(d)/(dt)log(1+t^(2))
02:01View SolutionFor xA→yB
log(d[A]dt)=log(+d[B]dt)+0.3010
Which of the followign reaction given relation is true?04:35View SolutionFor the reaction: aA + bB rarr cC+dD Rate = (dx)/(dt) = (-1)/(a)(d[A])/(dt) = (-1)/(b)(d[B])/(dt) = (1)/( c)(d[C])/(dt) = (1)/(d)(d[D])/(dt) In the following reaction, xA rarr yB log.[-(d[A])/(dt)] = log.[(d[B])/(dt)] + 0.3 where negative isgn indicates rate of disappearance of the reactant. Thus, x:y is:
View SolutionFor a chemical reaction aArarr bB , log[-(d(A))/(dt)]=log[(d[B])/(dt)]+0.3 Then find the approximately ratio of a and b is.
04:20View SolutionThe rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
For the reaction, aA→bB,
log[−dAdt]=log[dBdt]+0.6, then a:b is:04:25View SolutionFor the reaction aA+bB→cC, if −3d[A]dt=−d[B]dt=+1.5d[C]dt, then a, b and c respectively are
03:48View SolutionFor the reaction : xArarryB , "log"_(10)((-d[A])/(dt))="log"_(10)((+d[B])/(dt))+0.3 If the value of log_(10)5=0.7 , the value of x : y is :
04:37View SolutionThe rate and mechanism of chemical reactions are studied in chemical kinetics. The elementary reactions are single step reactions having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA + bB rarr cC + dD is given as : rate = =((dx)/(dt))=-(1)/(a) (d[A])/(dt) =-(1)/(b) (d[B])/(dt) =(1)/(c)(d[C])/(dt)=(1)/(d) (d[D])/(dt) or rate =K [A]^(a) [B]^(b) . In case of reversible reactions net rate expression can be written as : rate = K_(1)[A]^(a)[B]^(b) – K_(2)[C]^(c)[D]^(d) . At equilibrium, rate = 0. The constants K, K_(1), K_(2) , are rate constants of respective reaction. In case of reactions governed by two or more steps reactions mechanism, the rate is given by the solwest step of mechanism. For the reaction : aA rarr bB , log [(-dA)/(dt) ]=log [(dB)/(dt)]+0.6," then "a:b is :
04:34View SolutionFor the reaction : 3A_((g))rarr 2B_((g)) , the rate of formation of 'B' at 298 K is represented as ln((d[B])/(dt))=-4.606+2ln[A] . The order of reaction is
03:14View SolutionIn the reaction x A rarr yB, log{-(d[A])/(dt)}=log{+(d[B])/(dt)}+0.3 Then, x:y is
04:56View Solution

