An organic compound undergoes first order decomposition. The time taken for its decomposition to 1/8 and 1/10 of its initial concentration are and respectively. What is the value of
? Solution in Telugu
The correct Answer is:9
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - PRACTICE SHEET-1 (SINGLE OR MORE THAN ONE OPTION QUESTIONS)
16 Videos
- CHEMICAL KINETICSBOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - PRACTICE SHEET-1 (LINKED COMPREHENSION TYPE QUESTIONS)
6 Videos
- CHEMICAL KINETICSBOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - LEVEL-II(LECTURE SHEET EXERCISE-III MATCH THE FOLLOWING QUESTIONS)
3 Videos
- CHEMICAL KINETCSBOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETCSEXERCISE - EXERCISE - 3.2
45 Videos
- CHEMICAL THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - CHEMICAL THERMODYNAMICSEXERCISE - Additional Practice Exercise
54 Videos
Similar Questions
For the reaction N2+3H2→2NH3 , the rate d[NH3]dt=2×10−4Ms−1. Therfore the rate −d[N2]dt is given
View SolutionThe instantaneous rate of an elementary chamical reactkon aA+bB⇔cC+dD can be given by rate =Kf[A]a[B]b−Kb[C]c[D]d where Kf and Kb are rate constants for forward and backward reactions respectively for the reversible reaction. If the reaction is an irreversible one, the rate is expressed as, rate =K[A]a[B]b where K is rate contant for the given irreversible rate of disappearance of A is a/b times the rate of disappearance of B. The variation of rate constant K with temperature is expressed in terms of Arrhenius equation: K=Ae−Ea/RT whereas the ratio KfKb is expressed in terms of van't Hoff isochore: KfKb=Ae−ΔH/RT, where Ea and ΔH are energy of activation and heat of reaction respectively.
The variation of rate constant K and KfKb with temperature shows the following effects:
For endothrmic reaction when T increases then K increases and KfKb also increases.
(ii) For endothemic reaction when T decreases then K decreases and KfKb also decreases.
(iii) For exothermic when T increases then K and KfKb both increases.
(iv) For exothermic reaction when T decreases then K increases and KfKb decrease.
(v) For exothermic reaction when T increases thenK and KfKb both decrease.
View SolutionMatch the following columns
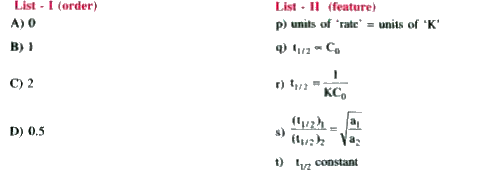
View SolutionDiscuss on the kinetic spontaneity of a chemical reaction. Is a slow reaction spontaneous? Why?
View SolutionWhich among the following is not an exact differential?
View SolutionIf in an AP,t_(1)=log_(10)a,t_(n+1)=log_(10)b and t_(2n+1)=log_(10) then a,b,c are in
View SolutionAn organic compound undergoes first decompoistion. The time taken for its decompoistion to 1//8 and 1//10 of its initial concentration are t_(1//8) and t_(1//10) , respectively. What is the value of ([t_(1//8)])/([t_(1//10)]) xx 10 ? (log_(10)2 = 0.3)
View SolutionThe first order rate constant for the decomposition of N_(2)O_(5) is 6.2 xx 10^(-4) sec^(-1) . The t_(1//2) of decomposition is
View SolutionAn organic compound undergoes first order decomposition. The time taken for the decomposition of 1/8 and 1/10 of its initial concentration are 1/8 and 1/10 respectively. What is the value of t1/8[t1/10]×10 (take log102=0.3)
View SolutionAn organic compound undergoes first-order decomposition . The time taken for its decomposition to 1/8 and 1/10 of its initial concentration are t_(1//8) and t_(1//10) respectively . What is the value of ([t_(1//8)])/([t_(1//10)]) xx 10 (take log_(10) 2 = 0.3 )
View SolutionObtain a relation log10.k2k1=Ea(T2−T1)2.303R×T1×T2
obtain a relation showing variation in rate constant with temeprature .
View SolutionA first order decomposition reaction takes 40 minutes for 30% decomposition. Calculate its t1/2 value.
View SolutionAn organic compound undergoes first-order decomposition. The time taken for its decomposition to 1//8 and 1//10 of its initial concentration are t_(1//8) and t_(1//10) respectively. What is the value of ([t_(1//8)])/([t_(1//10)])xx10?(log_(10)2=0.3)
View SolutionThe decomposition of a compound follows the rate law of a first order reaction. For the initial concentration of the compound to drop to (1)/(8) and (1)/(10) th of this value , times required are t_(1//8)th and t_(1//10) respectively. Find the value of (t_(1//8)/(t_(1//10))xx10). ["given":log"10^(2)=0.3]
View SolutionAn organic compound undergoes first decompoistion. The time taken for its decompoistion to 1/8 and 1/10 of its initial concentration are t1/8 and t1/10, respectively. What is the value of [t1/8][t1/10]×10? (log102=0.3)
View Solution
