Suppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E2)=12andP(E1∣E2)=14. Observe the lists given below :
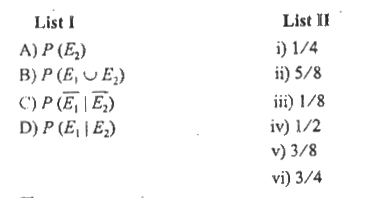
The correct matching of the list I from the list II is :Solution in Telugu
ABCDiiiiivii
ABCDivvvii
ABCDiviivii
ABCDiiiiiiiv
The correct Answer is:C
Step by step video solution for Suppose that E_1 and E_2 are two events of a random experiment such that P(E_(1))=1/4 , P(E_2 |E_2) =1/2 and P(E_1 |E_2)=1/4. Observe the lists given below : The correct matching of the list I from the list II is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBOOK - AAKASH SERIESCHAPTER - PROBABILITYEXERCISE - Practise Exercise
165 Videos
- PROBABILITYBOOK - AAKASH SERIESCHAPTER - PROBABILITYEXERCISE - Exercise-I
125 Videos
- PERMUTATIONS & COMBINATIONSBOOK - AAKASH SERIESCHAPTER - PERMUTATIONS & COMBINATIONSEXERCISE - PRACTICE EXERCISE
163 Videos
- QUADRATIC EQUATIONS & EXPRESSIONSBOOK - AAKASH SERIESCHAPTER - QUADRATIC EQUATIONS & EXPRESSIONSEXERCISE - PRACTICE EXERCISE
88 Videos
Similar Questions
The probability that a non leap year will have 53 Wednesdays is
View SolutionThe probability that a leap year have 53 sundays is………..
View SolutionIF 10pr=5040 then r=
View SolutionIf 3x+22x+3=4x+33x+4, then x =
View SolutionStatement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1
View SolutionE1,E2 are events of a sample sapce such that P(E1) =1/4 , P(E2∣E1)=1/2,P(E1∣E2)=1/4. Then P(E1∣E2)+P(E1∣¯¯¯¯E2)=
View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E2)=12andP(E1∣E2)=14. Observe the lists given below :
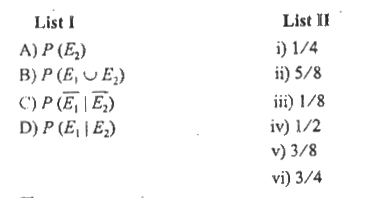
The correct matching of the list I from the list II is :
View SolutionSuppose E1 and E2 are two events of a sample space such that P(E1)=12,P(E2∣E1)=12,P(E1∣E2)=14 then P(E'2)= _____
View SolutionFill in the Blanks :
If E1 and E2 are independent events, then P(E1 ∩ E2) =..
View SolutionStatement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1
View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
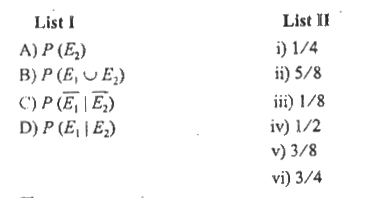
The correct matching of the list I from the list II is :
View SolutionIf E_1 and E_2 are two independent events associated with an experiment, then show that P(E_1cupE_2)=1-P(E_1^c)P(E_2^c)
View SolutionIf E1 and E2 are independent events associated with an experiment such that P(E1)=P1 and P(E2)=P2. Find
P(E1andE2).
View SolutionIf E_1 and E_2 are independent events associated with an experiment such that P(E_1)=P_1 and P(E_2)=P_2 . Find P(E_1 but not E_2) .
View SolutionIf E_1 and E_2 are independent events associated with an experiment such that P(E_1)=P_1 and P(E_2)=P_2 . Find P( neither E_1 nor E_2) .
View SolutionIf E1 and E2 are independent events associated with an experiment such that P(E1)=P1 and P(E2)=P2. Find
P(E1orE2).
View Solution
