Consider an electric field →E=E0ˆx, where E0 is a constant. The flux through the shaded area (as shown in the figure) due to this field is

2E0a2
√2E0a2
E0a2
E0a2√2
The correct Answer is:C
Here, →E=E0ˆx
In this problem, ˆx,ˆy and ˆz are the unit vectors along x, y and z-axes respectively.
∴ Shaded area, →A=−−→PQ×−→PS
→A=(0ˆx+aˆy+0ˆz)×(aˆx+0ˆy+aˆz)=(a2ˆx−a2ˆz)
ϕε=→E.→A=(E0ˆx).(a2ˆx−a2ˆz)=E0a2

Topper's Solved these Questions
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET ITALS
1 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET VITALS
18 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- ELECTRONIC DEVICESBOOK - MTG GUIDECHAPTER - ELECTRONIC DEVICESEXERCISE - AIPMT/NEET (MCQs)
42 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
Similar Questions
Knowledge Check
Conisder an electric field →E=E0ˆx where E0 is a constant .
The flux through the shaded area (as shown in the figure) due to this field is
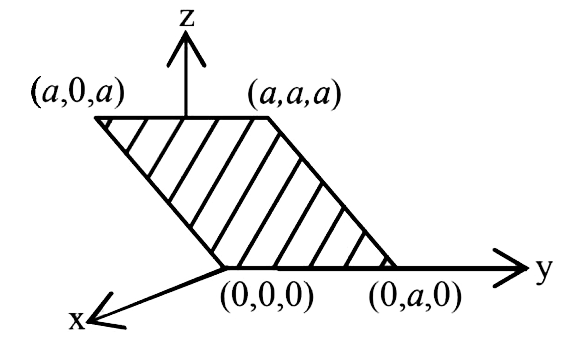 A(a) 2E0a2B(b) √2E0a2C(c) E0a2D(d) E0a2√2
A(a) 2E0a2B(b) √2E0a2C(c) E0a2D(d) E0a2√2If →E=E0Xaˆi(x−mt) then flux through the shaded area is:
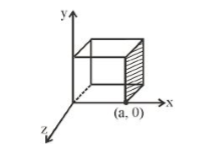 AE0a2BZeroCE0a3D−E0a3
AE0a2BZeroCE0a3D−E0a3The potential field of an electric field →E=(yˆi+xˆj) is
AV=−xy+constantBV=−(x+y)+ constantCV=−(x2+y2)+ constantDV = constant
Find the potential V of an electrostatic field →E=a(yˆi+xˆj), where a is a constant.
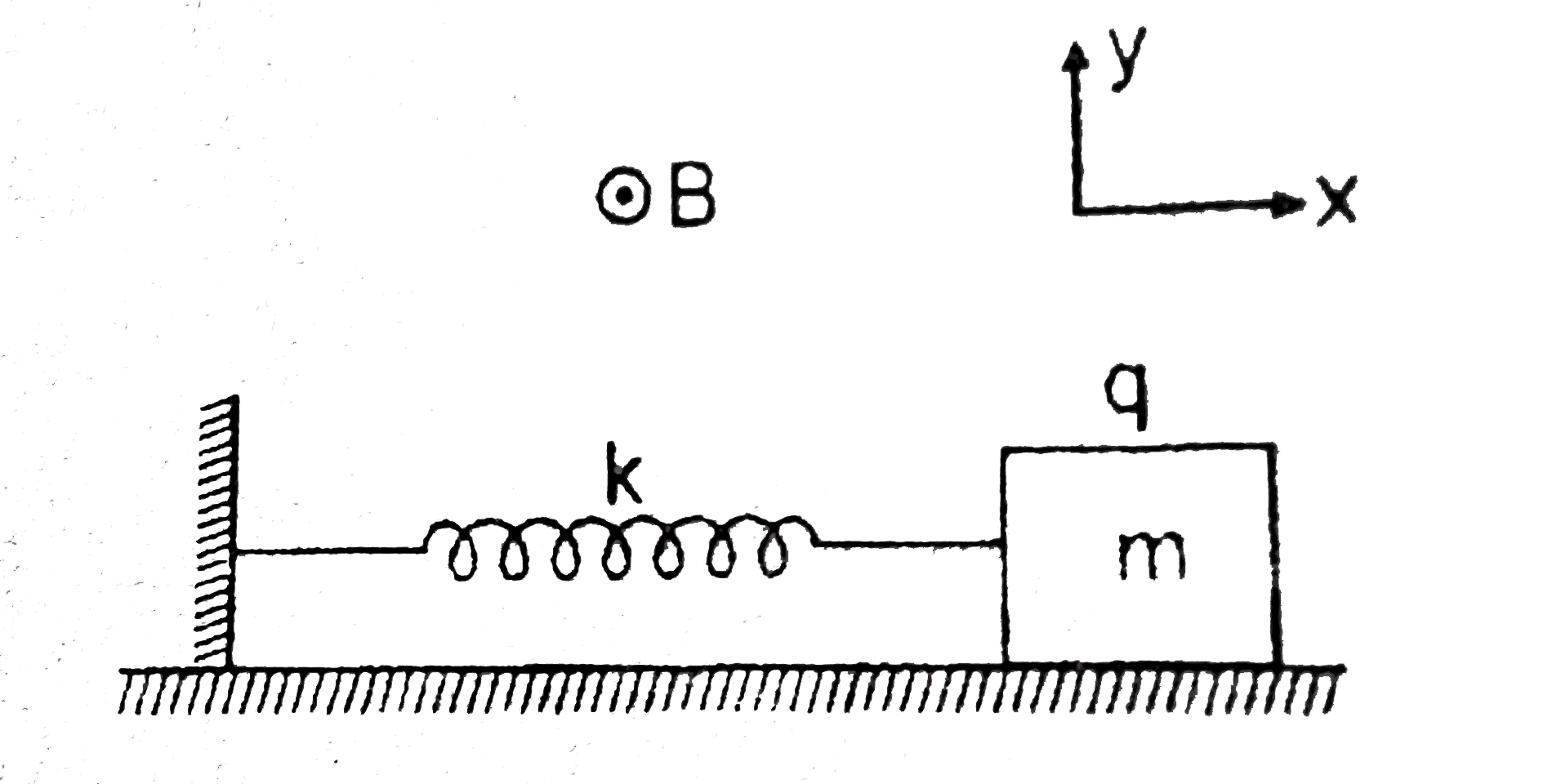
View SolutionA spring of spring constant 'K' is fixed at one end has a small block of mass m and charge q is attached at the other end. The block rests over a smooth horizontal surface. A uniform and constant magnetic field B exists normal to the plane of paper as shown in figure. An electric field →E=E0ˆi(E0 is a positive constant) is switched on at t=0 sec. The block moves on horizontal surface without ever lifting off the surface. Then the normal reaction acting on the block is :
View SolutionThe potential field of an electric field →E=(yˆi+xˆj) is
View SolutionFind the potential V of an electrostatic field →E=a(yˆi+xˆj), where a is a constant.
View SolutionA spring of spring constant 'K' is fixed at one end has a small block of mass m and charge q is attached at the other end. The block rests over a smooth horizontal surface. A uniform and constant magnetic field B exists normal to the plane of paper as shown in figure. An electric field →E=E0ˆi(E0 is a positive constant) is switched on at t=0 sec. The block moves on horizontal surface without ever lifting off the surface. Then the normal reaction acting on the block is :

View Solution
