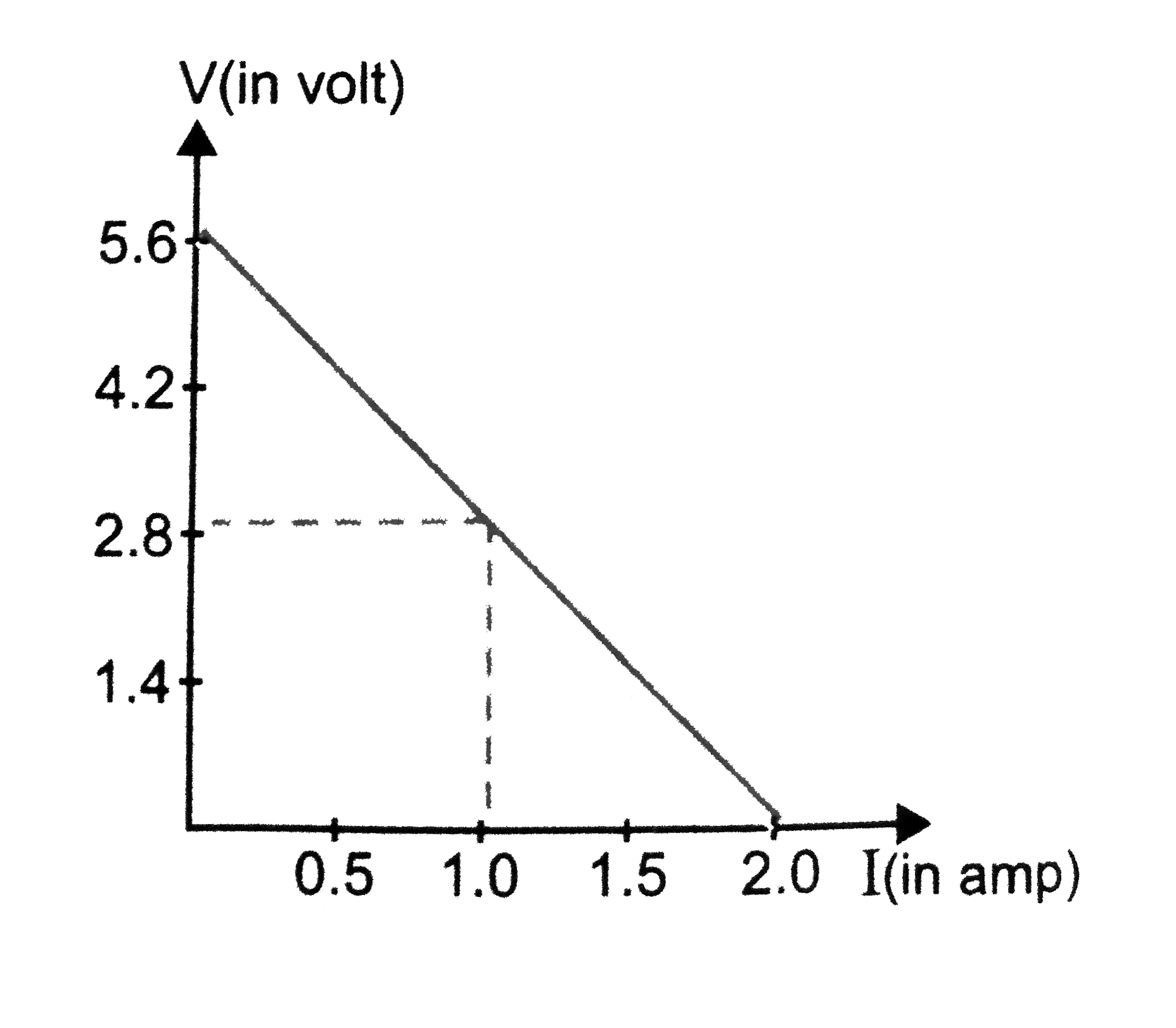
Four cells of identical emf ε and internal resistance r are connected in series to a variable resistor. The following graph shows the variation of terminal voltage of the combination with current. The emf of each cell used is

1.4 V
5.6 V
2 V
1 V
The correct Answer is:A
Emf of each cell =ε
Internal resistance of each cell = r
Number of cells (n) = 4
Total emf = nε=4ε
Total internal resistance = nr=4r
Terminal voltage,
V=4ε−I(4r) ...(i)
from the graph,
When I=0,V=5.6V
∴ From (i),
5.6=4ε−0
ε=5.64=1.4V

Topper's Solved these Questions
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - CHECK YOUR NEET VITALS
16 Videos
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - MCQs AIPMT / NEET
32 Videos
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - MCQs AIPMT / NEET
32 Videos
- ATOMS AND NUCLEIBOOK - MTG GUIDECHAPTER - ATOMS AND NUCLEIEXERCISE - AIPMT/NEET(MCQs)
40 Videos
- DUAL NATURE OF MATTER AND RADIATION BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs
30 Videos
Similar Questions
4 cells of identical emf E and internal resistance r, are connected in series to a variable resistor. The following graph shows the variation of termical voltage of the combination with the current output. Fig. MTP 1.2.
(a) What is the emf of each cell used?
(b) For what current from the cells, does maximum power dissipation occur in the circuit?
(c) Calculate the internal resistance of each cell.
View Solution.A cell of emf E and internal resistance r is connected across a variable resistor. Plot a graph showing variation of terminal voltage V of cell versus the current.
View Solution
Knowledge Check
A cell of emf ε and internal resistance r is charged by a current I, then
Athe cell stores chemical energy at the rate of εiBthe cell stores chemical energy at the rate of i2rCthe cell stores chemical energy at the rate of εI−i2rDthe storage of chemical energy rate cannot be calculatedA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
A(1n)B1(n+1)Cn(n+1)D(n+1)nA cell of emf 'E' and internal resistance 'r' is connected to a variable external resistor 'R'. The graph which gives the terminal voltage of cell 'V' with respect to R is :
A B
B C
C D
D
A cell of emf ε and internal resistance r is connected across a variable resistor R. Plot a graph showing variation of terminal voltage V of the cell versus the current I. Using the plot, show how the emf of the cell and its internal resistance can be determined.
View SolutionA cell of emf ε and internal resistance r is connected across a variable resistor R. Plot a graph showing variation of terminal voltage V of the cell versus the current I. Using the plot, show how the emf of the cell and its internal resistance can be determined.
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View SolutionA cell of emf 'ε' and internal resistance 'r' is connected across a variable resistor 'R'. Plot a graph showing variation of terminal voltage 'V' of the cell versus the current 'l'. Using the plot, show how the emf of the cell and its internal resistance can be determined.
View SolutionA cell of emf ε and internal resistance (r) is connected in series with an external resistance (nr) then the ratio of the terminal potential difference to emf is:
View Solution
