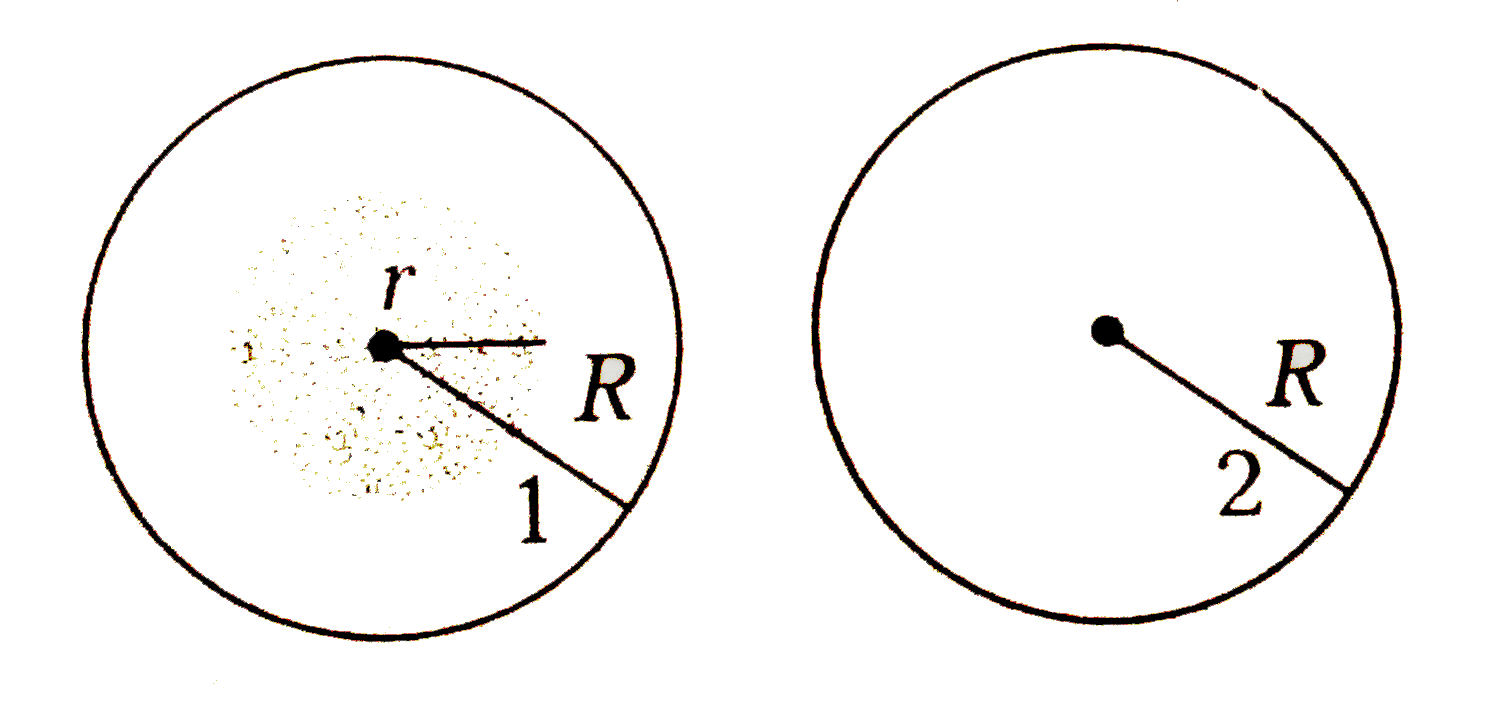
A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate $\frac{d \to B}{d t} .$ Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in the figure. Then the e.m.f. generated is

A

zero in loop 1 and zero in loop 2

B

$- \frac{d \to B}{d t} π r^{2}$ in loop 1 and $- \frac{d \to B}{d t} π r^{2}$ in loop 2

C

$- \frac{d \to B}{d t} π R^{2}$ in loop 1 and zero in loop2

D

$- \frac{d \to B}{d t} π r^{2}$ in loop 1 and zero in loop 2

Text Solution

Verified by Experts

The correct Answer is:D

Emf generated in loop 1,
$ε_{1} = - \frac{d ϕ}{d t} = - \frac{d}{d t} (\to B . \to A) = - \frac{d}{d t} (B A) = - A \times \frac{d B}{d t}$
$ε_{1} = - (π r^{2} \frac{d B}{d t})$
Emf generated in loop 2.
$ε_{2} = - \frac{d}{d t} (B A) = - \frac{d}{d t} (0 \times A) = 0$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate $\frac{d B}{d t}$ . Loop 1 of radius R $>$ r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is

A $- \frac{d \to B}{d t} π R^{2}$ in loop 1 and zero in loop 2
B $- \frac{d \to B}{d t} π r^{2}$ in loop 1 and zero in loop 2
CZero in loop 1 and zero in loop 2
D $- \frac{d \to B}{d t} π r^{2}$ in loop 1 and $- \frac{d \to B}{d t} π r^{2}$ in loop 2
Question 2 - Select One
A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate $\frac{d B}{d t}$ . Loop 1 of radius R $>$ r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is

AZero in loop 1 and zero in loop 2
B $- \frac{d B}{d t} π r^{2}$ in loop 1 and $- \frac{d B}{d t} π^{2}$ in loop 2
C $- \frac{d B}{d t} π R^{2}$ in loop 1 and zero in loop 2
D $- \frac{d B}{d t} π r^{2}$ in loop 1 and zero in loop 2
Question 3 - Select One
A conducting loop is pulled with a constant velocity towards a region of uniform magnetic field as shown in the figure then the current involved in the loop is ( $d > r$ ) -

AClockwise while entering
BAnticlockwise while entering
CZero when partially outside
DAnticlockwise while leaving.

MTG GUIDE-ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS-AIPMT/NEET MCQS

Home
Ask Doubt
Profile