A metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
4.5 cm
6.75 cm
1.5 cm
7.5 cm
The correct Answer is:C
Here, μ=43, Real debth=6 cm
μReal debthApparent debth
Apparent debth = 64/3=184=4.5 cm
The coin will appear to be raised = 6 cm −4.5 cm = 1.5 cm
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - Check your NEET vitals25videos
OPTICS
- BOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET55videos
OPTICS
- BOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET55videos
OPTICS
- BOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)48videos
MAGNETIC EFFECTS OF CURRENT AND MAGNETISM
Similar Questions
The apparent depth of an object at the bottom of tank filled with a liquid of refractive index 1.3 is 7.7 cm. what is the actual depth of the liquid in the tank ?
View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?
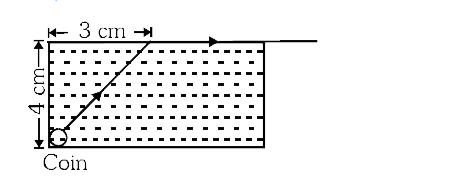
View Solution
Knowledge Check
- Question 1 - Select One
A small coin is resting on the bottom of a beaker filled with liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface. How fast is the light travelling in the liquid?
 A2.4×108ms−1B3.0×108ms−1C1.2×108ms−1D1.8×108ms−1
A2.4×108ms−1B3.0×108ms−1C1.2×108ms−1D1.8×108ms−1 - Question 2 - Select One
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?

A1.8×108ms−1B2.4×108ms−1C3.0×108ms−1D1.2×108ms−1 - Question 3 - Select One

A real image of an object is formed by a conex lens at the bottom of an empty beaker. The beaker is now filled with a liquid of refractive index 1.4 to a depth of 7 cm. In order to get the image again at the bottom the beaker shoud be movedAdownward by 2 cmBupward by 2 cmCdownward by 3 cmDupward by 3 cm
An object is placed at the bottom of a tank filled with liquid of refractive index 1.6. If the actual depth of the tank is 10 cm, what will be the apparent depth of the object?
View SolutionA point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)
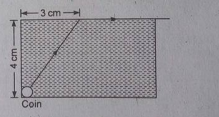
How fast is the light travelling in the liquid ?View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)

How fast is the light travelling in the liquid ?View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels up to the surface of the liquid and moves along its surface (see figure ).
How fast is the light travelling in the liquid ?
 View Solution
View Solution

