A metal plate is lying at the bottom of a tank full of a transparent liquid. Height of tank is 100 cm but the plate appears to be at 45 cm above bottom. The rerfractive index of liquid is
1.00
1.53
1.81
1.32
The correct Answer is:C
To find the refractive index of the liquid in which a metal plate is submerged, we can use the relationship between the real depth (D) and the apparent depth (D') of the object.
1. Identify the Given Values:
- Height of the tank (D) = 100 cm (this is the real depth)
- Apparent depth (D') = 45 cm above the bottom of the tank.
- Therefore, the distance from the top of the liquid to the plate is:
D′=100cm−45cm=55cm
2. Understand the Relationship:
The relationship between real depth (D) and apparent depth (D') is given by the formula:
D′=μ2μ1⋅D
where:
- μ1 = refractive index of the liquid (unknown)
- μ2 = refractive index of air = 1 (since air is the medium above the liquid)
3. Substituting Known Values:
Since μ2=1, we can rewrite the equation:
D′=1μ1⋅D
Rearranging gives:
μ1=DD′
4. Plugging in the Values:
Now substitute the values of D and D':
μ1=100cm55cm
5. Calculating the Refractive Index:
Performing the division:
μ1=10055≈1.8181
6. Final Result:
The refractive index of the liquid is approximately:
μ1≈1.81
Conclusion:
The refractive index of the liquid is approximately 1.81.
- Height of the tank (D) = 100 cm (this is the real depth)
- Apparent depth (D') = 45 cm above the bottom of the tank.
- Therefore, the distance from the top of the liquid to the plate is:
D′=100cm−45cm=55cm
The relationship between real depth (D) and apparent depth (D') is given by the formula:
D′=μ2μ1⋅D
where:
- μ1 = refractive index of the liquid (unknown)
- μ2 = refractive index of air = 1 (since air is the medium above the liquid)
Since μ2=1, we can rewrite the equation:
D′=1μ1⋅D
Rearranging gives:
μ1=DD′
Now substitute the values of D and D':
μ1=100cm55cm
Performing the division:
μ1=10055≈1.8181
The refractive index of the liquid is approximately:
μ1≈1.81
The refractive index of the liquid is approximately 1.81.
Topper's Solved these Questions
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - Topicwise Practice Questions
200 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
Similar Questions
A jar 15cm long is filled with a transparent liquid. When viewed from the top, its bottom appears to be 12cm below. What is the refractive index of the liquid ?
View SolutionThe depth of water in a bucket is 40 cm but its bottom appears to be raised by 10 cm. what is the refractive index of water ?
View Solution
Knowledge Check
The pressure at the bottom of a tank containing a liquid does not depend on
AAcceleration due to gravityBHeight of the liquid columnCArea of the bottom surfaceDNature of the liquidThe pressure at the bottom of a tank containing a liquid does not depend on
AAcceleration due to gravityBHeight of the liquid columnCArea of the bottom surfaceDNature of the liquidThe pressure at the bottom of a liquid tank does not depend on :
AAcceleration due to gravityBdensity of the liquidCheight of the liquidDarea of the liquid surface
The pressure at the bottom of a tank of liquid is not proprtional to
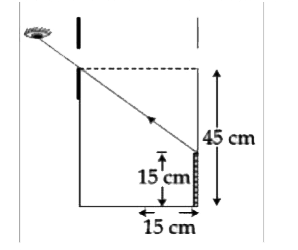
View SolutionAn observer can see through a small hole on the side of a jar (radius 15 cm) at a point at height of 15 cm from the bottom (see figure). The hole is at a height of 45 cm. When the jar is filled with a liquid up to a height of 30 cm the same observer can see the edge at the bottom of the jar. If the refractive index of the liquid is N/100, where N is an integer, the value of N is ___________.
View SolutionA tank of height 50 m is filled with oil fully. If the bottom of the tank appears to be 40 m below its top, the refractive index of the oil should be
View SolutionA mark at the bottom of a liquid appears to rise by 0.1m. The depth of the liquid is 1m. The refractive index of the liquid is
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
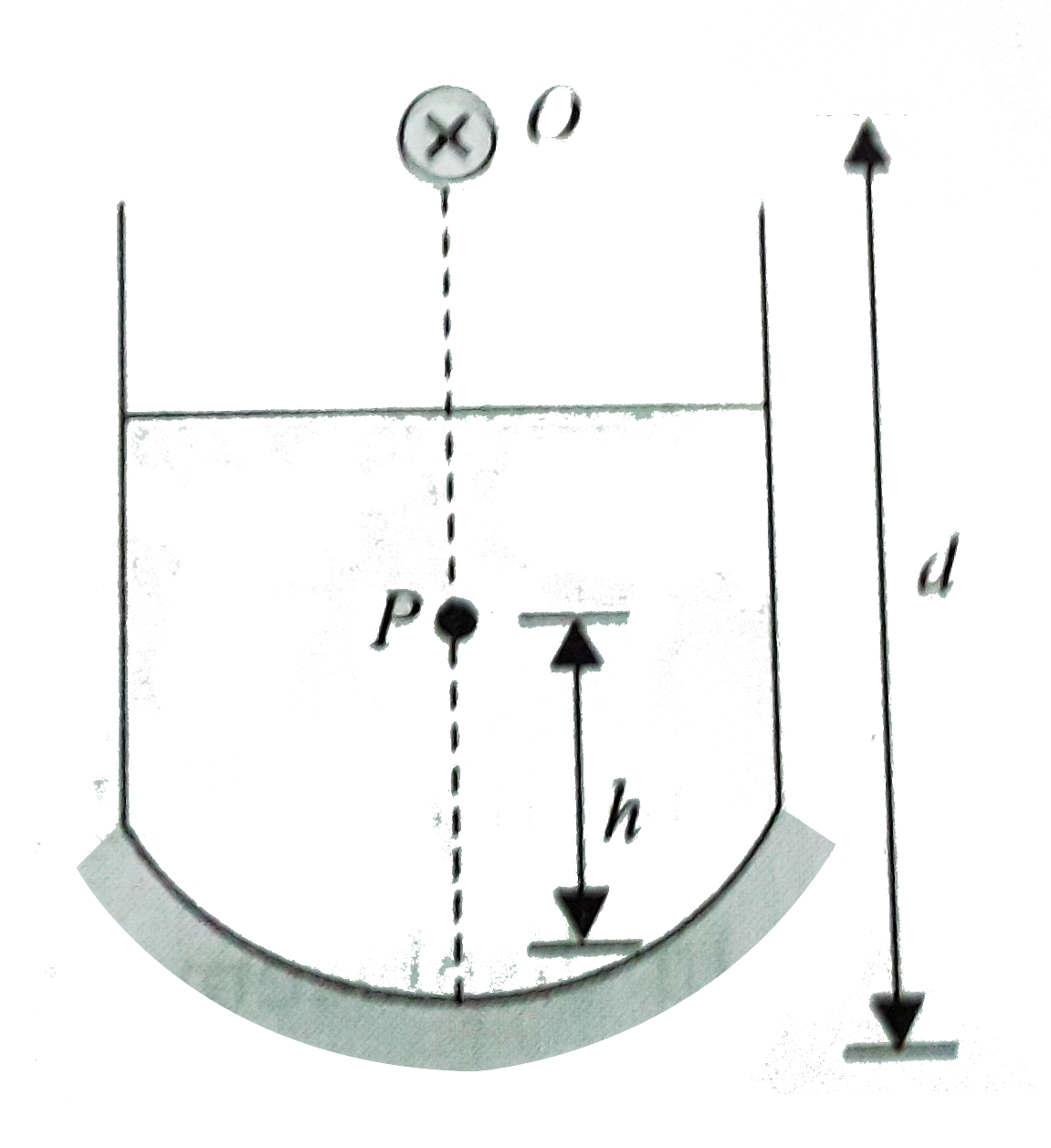
View Solution
