A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
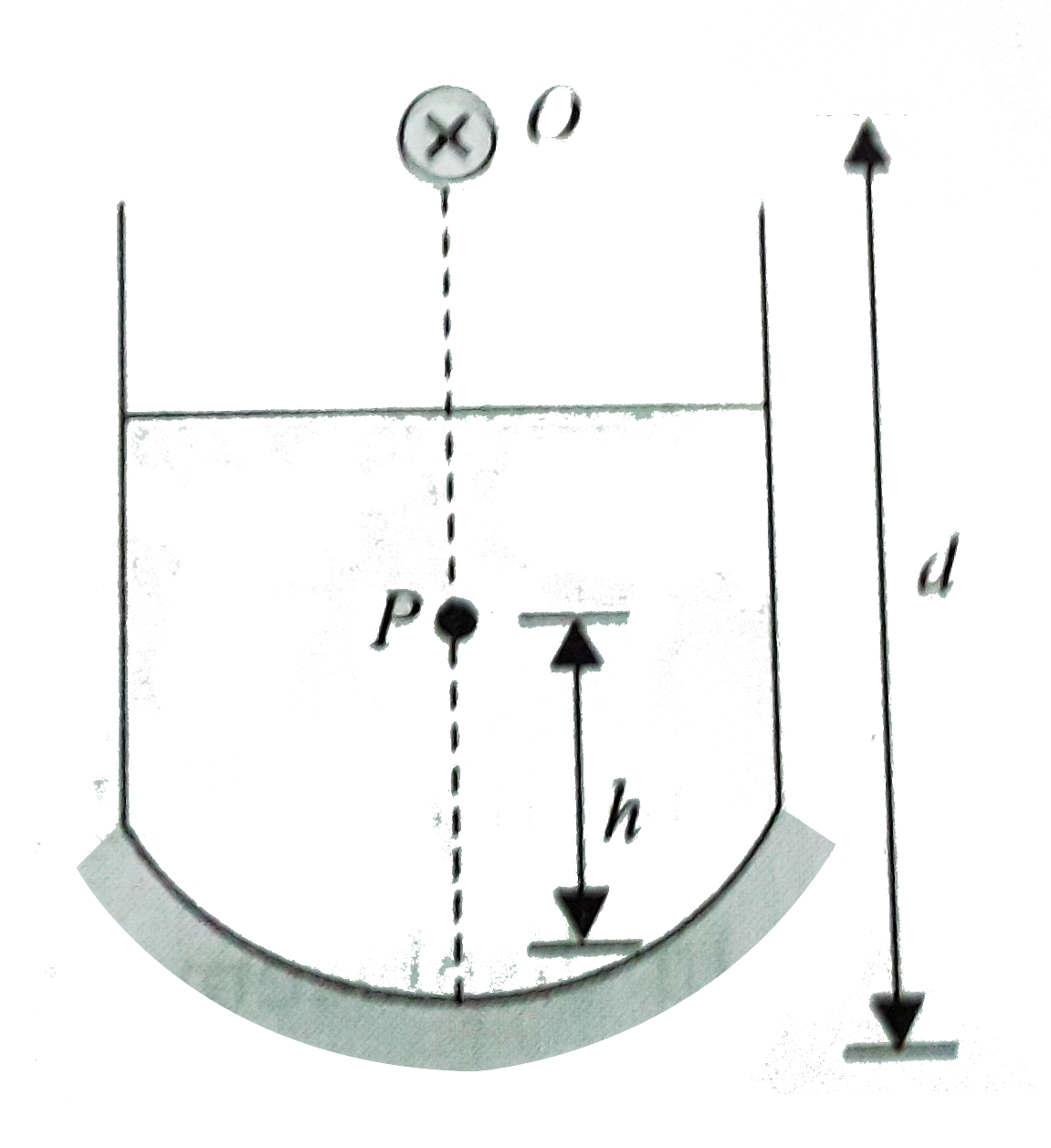
h(1−1μ)
2hμ−1
zero
2hμ
The correct Answer is:c.
There will be two images on by direct observation other by reflection through mirror.
Apparent depth
=Real depthμrel
=Real depth(μincidentμrefractive)=(d−h)(μ/1)
dapp=(d−h)μ
Object P is placed at the center of curvature of the mirror. Its image will be formed at P itself.
So, for image also,
dapp=(d−h)μ−(d−h)μ=0

Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
An object is placed at the bottom of a tank filled with liquid of refractive index 1.6. If the actual depth of the tank is 10 cm, what will be the apparent depth of the object?
View SolutionIn Fig. a plane mirror lies at a height h above the bottom of a beaker containingwater (refractive index μ) upto a height f. Find the position of the image of the
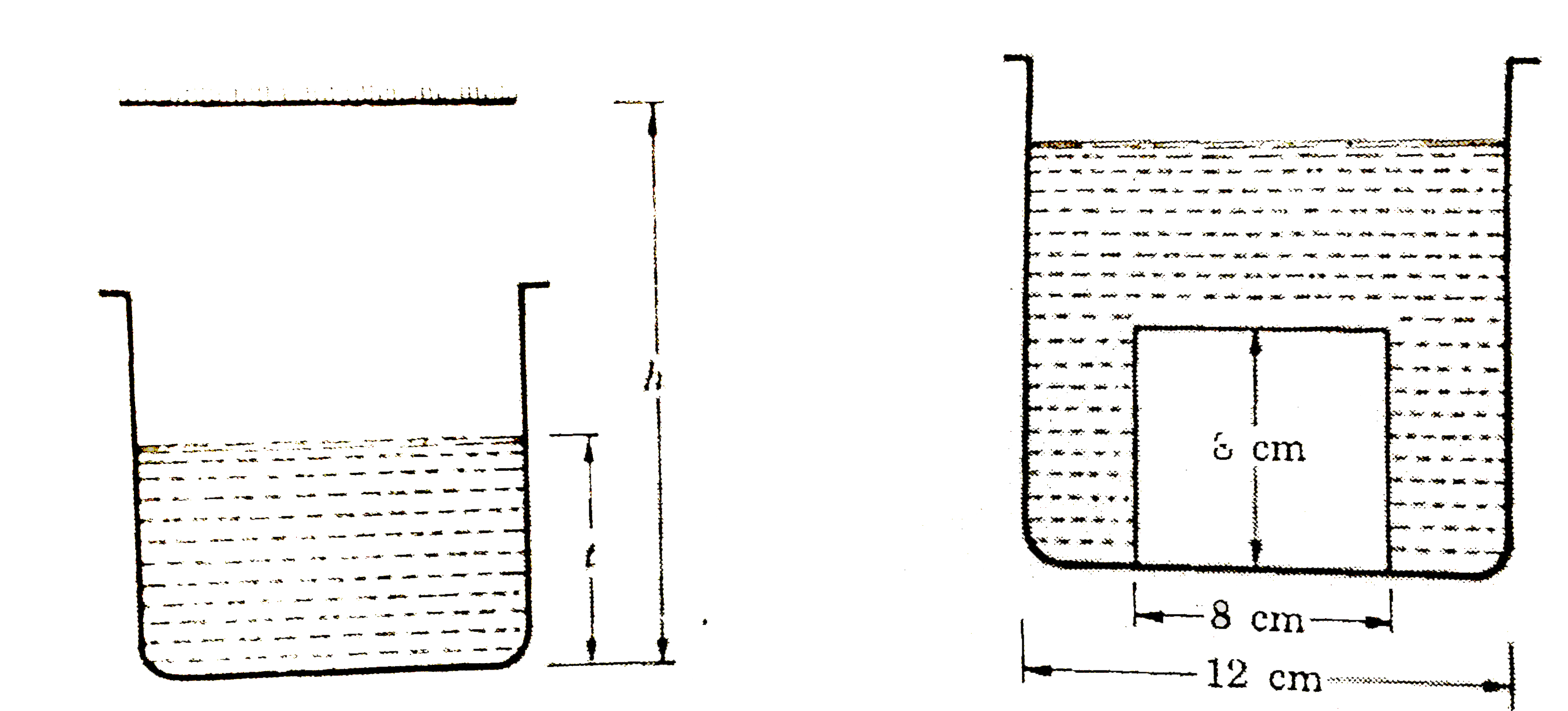
View Solution
Knowledge Check
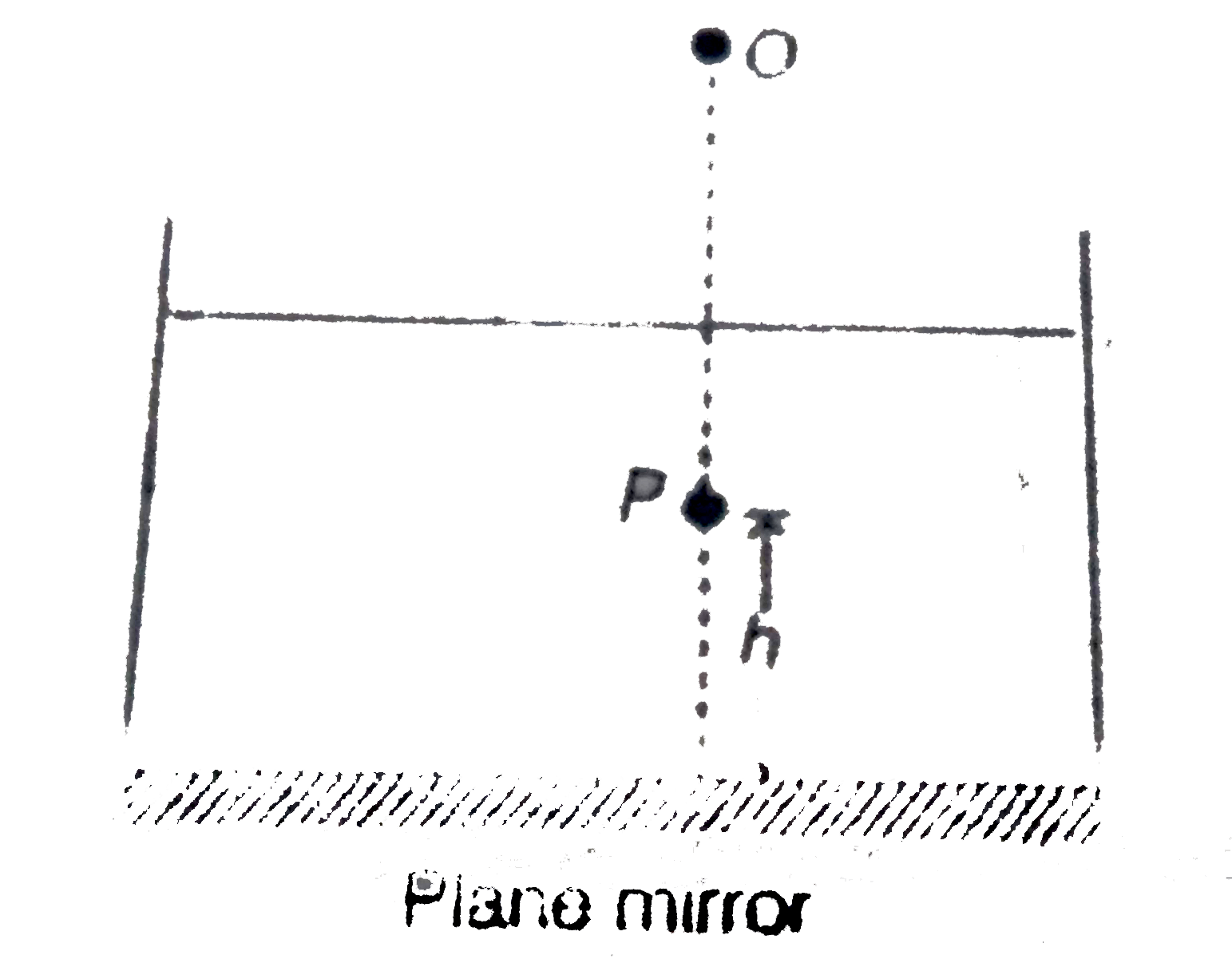
A plane mirror is placed at the bottom of the tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observer O-vertically above P outside the liquid see P and its image in the mirror. The apparent distance between these two will be:
 A2μhB2hμC2gμ−1Dh(1+1μ)
A2μhB2hμC2gμ−1Dh(1+1μ)A plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observes P and its image in the mirror. The apparent distance between two will be
 A2μhB2hμC2hμ−1Dh(1+1μ)
A2μhB2hμC2hμ−1Dh(1+1μ)There is a plane mirror at the bottom of tank filled with water having refractive index 4/3. A point object is placed at a height 10 cm above the bottom. What will be the apparent distance between point object and its image in plane mirror as observed by an observer outside the liquid in air ? Line joining observer and object is normal to the surface of water.
A10 cmB15 cmC20 cmD25cm
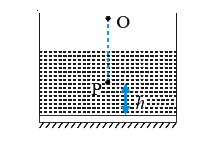
A tank contains a transparent liquid of refractive index μ. The bottom of the tank is a plane mirror as shown. A person at P looks at an object O and its image in the mirror. The distance between the object and its image in the mirror as preceived by the person is

View SolutionThe apparent depth of an object at the bottom of tank filled with a liquid of refractive index 1.3 is 7.7 cm. what is the actual depth of the liquid in the tank ?
View SolutionA small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index μ upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut- off the light from the bulb.
View SolutionA concave mirror of radius R is kept on a horizontal table. Water (refractive index =mu.) is poured into it up to a height h. Where should an object be placed so that its image is formed on itself ?

View SolutionAn object is placed 21 cm in front of a concave mirror of radius of curvature 10cm. A glass slab of thickness 3cm and refractive index 1.5 is then placed close to the error in the space between the object and the mirror. The distance of the near surface of the slab from the mirror is 1cm. The final image from the mirror will be formed at
View Solution
