Work done upon a body is
a vector quantity
a scalar quantity
always positive
always negative
The correct Answer is:B
To solve the question "Work done upon a body is," we need to analyze the definition and characteristics of work done in physics. Let's break it down step by step:
Step 1: Understanding Work Done
Work done (W) on a body is defined as the product of the force (F) applied to the body and the displacement (S) of the body in the direction of the force. Mathematically, it can be expressed as:
W=F⋅S⋅cos(θ)
where:
- W is the work done,
- F is the magnitude of the force applied,
- S is the displacement of the body,
- θ is the angle between the force and the displacement vector.
Step 2: Work Done as a Scalar Quantity
Work done is a scalar quantity, meaning it has magnitude but no direction. This is important to note because it distinguishes work from vector quantities like force and displacement.
Step 3: Conditions for Work Done
1. Positive Work: Work is done positively when the force and displacement are in the same direction. For example, if a force is applied in the direction of the displacement, θ=0∘ and cos(0)=1, thus:
W=F⋅S⋅1=F⋅S
2. Negative Work: Work is done negatively when the force and displacement are in opposite directions. For instance, if the force is applied in the opposite direction to the displacement, θ=180∘ and cos(180)=−1, thus:
W=F⋅S⋅(−1)=−F⋅S
3. Zero Work: Work is zero when the force is perpendicular to the displacement. In this case, θ=90∘ and cos(90)=0, thus:
W=F⋅S⋅0=0
Step 4: Conclusion
From the analysis, we conclude that work done can be:
- Positive when force and displacement are in the same direction.
- Negative when force and displacement are in opposite directions.
- Zero when force is perpendicular to displacement.
Thus, the answer to the question "Work done upon a body is" can be summarized as follows:
- Work done is a scalar quantity.
- It can be positive, negative, or zero depending on the direction of force relative to displacement.
Work done (W) on a body is defined as the product of the force (F) applied to the body and the displacement (S) of the body in the direction of the force. Mathematically, it can be expressed as:
- W is the work done,
- F is the magnitude of the force applied,
- S is the displacement of the body,
- θ is the angle between the force and the displacement vector.
Work done is a scalar quantity, meaning it has magnitude but no direction. This is important to note because it distinguishes work from vector quantities like force and displacement.
1. Positive Work: Work is done positively when the force and displacement are in the same direction. For example, if a force is applied in the direction of the displacement, θ=0∘ and cos(0)=1, thus:
From the analysis, we conclude that work done can be:
- Positive when force and displacement are in the same direction.
- Negative when force and displacement are in opposite directions.
- Zero when force is perpendicular to displacement.
- Work done is a scalar quantity.
- It can be positive, negative, or zero depending on the direction of force relative to displacement.
Topper's Solved these Questions
Similar Questions
Knowledge Check
STATEMENT-1 Work done by static friction in any reference frame is zero
STATEMENT-2 If work done on the body is positive its kinetic energy increases.AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-9BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-9CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is TrueA body of mass 2 kg starts with an intitial-velocity 5 m/s. It the body is acted upon by a time dependent force (F) as shown in figure, then work done on the body in 20 s is
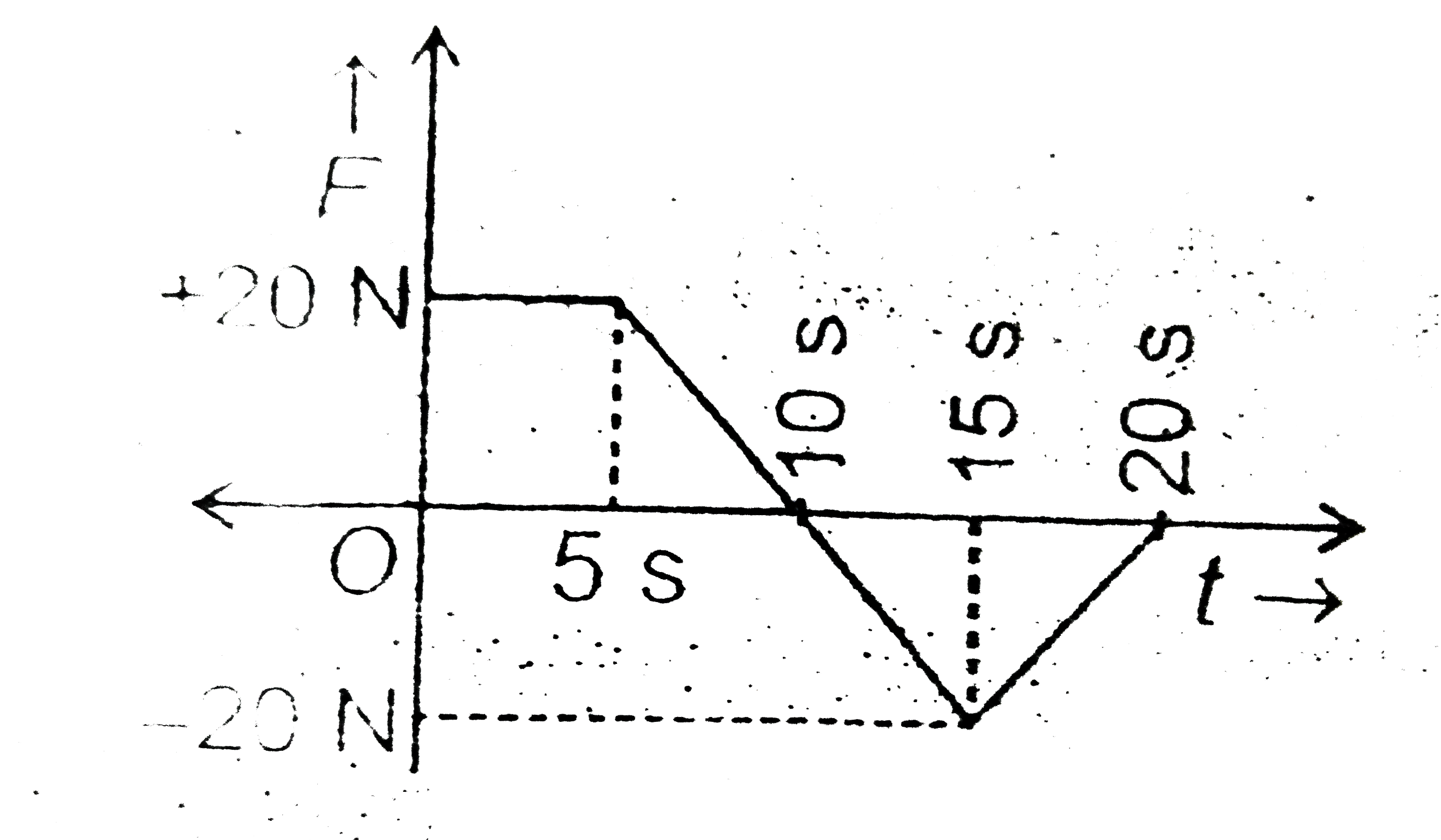 A−875JB875JC600 JD−600NJ
A−875JB875JC600 JD−600NJWhen work is done on a body by an external force, its
AOnly kinetic energy increasesBOnly potential energy increasesCBoth kinetic and potential energies may increaseDSum of kinetic and potential energies remains constant
The work done by a body is the product of force and :
View SolutionWrite the formula for work done on a body when the body moves at an angle to the direction of force. Give the meaning of each symbol used.
View SolutionA body starts from rest and acquires a velocity V in time T .The work done on the body in the time t is proportional to
View SolutionWhen work is done on a body by an external force, its
View SolutionSTATEMENT -1: Work don on a body A by B must be equal and opposite and the woek done by A on B
STATEMENT-2: if body undergoes a displacement under the action of a force, then the force must have done some work.
STATEMENT-3: When we climb the stairs, it is the work done by the stairs which increases our potential energy.
View Solution
